为什么均方误差损失函数可以用于线性回归？

动机与核心假设

我们先从问题的起点开始。在线性回归任务中，我们相信特征 x 和目标 y 之间存在一个近似的线性关系。然而，真实世界的数据总是充满着“不完美”，这种不完美我们称之为噪声（Noise）或误差（Error）。

因此，我们不奢求一个完美的线性模型 y = w^T*x + b，而是构建一个包含误差项 ε 的更现实的模型：

$$y={\mathbf{w}}^{\top }\mathbf{x}+b+ϵ$$

这里的 w^T*x + b 是我们模型的预测值，我们记为 ŷ。而 ε 就是真实值 y 和模型预测值 ŷ 之间的差距。

到目前为止，我们还无法确定用什么损失函数。关键的一步在于，我们必须对这个神秘的误差 ε 的性质做一个核心假设。

核心假设：

我们假设误差 ε 是独立同分布的，并且服从一个均值为0，方差为 σ² 的高斯分布（正态分布）。

$$ϵ\sim \mathcal{N}(0,{\sigma }^2)$$

这个假设为什么合理？在许多现实场景中，误差是由大量微小的、独立的随机因素共同造成的。根据中心极限定理，这些因素的综合影响往往会趋向于一个正态分布。比如，在测量房价时，测量的微小偏差、未考虑到的细微特征（如装修的新旧程度）等，这些都可以被看作是随机噪声。假设它们服从正态分布，是一个非常自然且方便的数学起点。

从概率到似然

既然我们已经假设了误差 ε 的分布，我们就可以推导出在给定输入 x 和模型参数 w, b 的情况下，观测到真实值 y 的概率密度。

因为 y = ŷ + ε，而 ε = y - ŷ，所以 y 的分布实际上就是以 ŷ 为均值的正态分布。

$$y\mid \mathbf{x};\mathbf{w},b\sim \mathcal{N}({\mathbf{w}}^{\top }\mathbf{x}+b,{\sigma }^2)$$

换句话说，对于一个给定的 x，我们的模型预测了一个值 ŷ，而真实值 y 在 ŷ 附近波动，波动的形态就是一个钟形曲线（高斯分布）。

这个概率的数学表达式（即高斯分布的概率密度函数）就是：

$$P(y\mid \mathbf{x};\mathbf{w},b)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{(y-({\mathbf{w}}^{\top }\mathbf{x}+b){)}^2}{2{\sigma }^2}\right)$$

现在，我们切换视角。在机器学习训练中，我们已经拥有了整个数据集 (X, Y) = {(x^(i), y^(i))}。我们的目标不再是预测 y 的概率，而是反过来去寻找一组最好的模型参数 w 和 b，使得我们观测到的这组数据出现的可能性（Likelihood）最大。

这就是最大似然估计（Maximum Likelihood Estimation, MLE） 的核心思想。

假设我们有 n 个独立的样本，那么整个数据集的似然函数就是所有单个样本似然的乘积：

$$L(\mathbf{w},b)=P(\mathbf{Y}\mid \mathbf{X};\mathbf{w},b)=\prod _{i=1}^{n}P(y^{(i)}\mid {\mathbf{x}}^{(i)};\mathbf{w},b)$$

最大化似然

我们的目标是找到 w 和 b 来最大化 L(w, b)。

$$\underset{\mathbf{w},b}{\mathrm{argmax}}\prod _{i=1}^n\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{(y^{(i)}-({\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}+b){)}^2}{2{\sigma }^2}\right)$$

直接对这个巨大的连乘积进行求导优化是非常困难的。指数函数的连乘会变得极其复杂，而且数值上非常容易下溢（underflow）变成零。

对数似然

为了解决这个问题，数学家们想出了一个绝妙的办法：取对数。因为 log 函数是单调递增的，所以最大化 L(w, b) 等价于最大化 log(L(w, b))。而对数可以将连乘运算转化为连加运算，大大简化了问题。

我们来对似然函数取对数，得到对数似然（Log-Likelihood）：

$$\log L(\mathbf{w},b)=\log \left(\prod _{i=1}^{n}P(y^{(i)}\mid {\mathbf{x}}^{(i)};\mathbf{w},b)\right)$$ $$=\sum _{i=1}^n\log P(y^{(i)}\mid {\mathbf{x}}^{(i)};\mathbf{w},b)$$ $$=\sum _{i=1}^n\log \left(\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{(y^{(i)}-({\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}+b){)}^2}{2{\sigma }^2}\right)\right)$$

利用对数性质 log(A*B) = log(A) + log(B) 和 log(exp(x)) = x，我们可以展开上式：

$$=\sum _{i=1}^n\left(\log \left(\frac{1}{\sqrt{2\pi {\sigma }^2}}\right)-\frac{(y^{(i)}-({\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}+b){)}^2}{2{\sigma }^2}\right)$$ $$=n\log \left(\frac{1}{\sqrt{2\pi {\sigma }^2}}\right)-\frac{1}{2{\sigma }^2}\sum _{i=1}^n(y^{(i)}-({\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}+b){)}^2$$

现在，我们的目标是最大化这个对数似然函数。观察上式，第一项 n log(...) 是一个常数，因为它不依赖于我们要优化的参数 w 和 b。第二项前面的 -1 / (2σ²) 也是一个负常数。

最大化一个 C - K * f(x) (其中 C 和 K 为正数) 就等价于最小化 f(x)。

因此，我们的目标从“最大化对数似然”转变成了“最小化”下面这个部分：

$$\underset{\mathbf{w},b}{\mathrm{argmin}}\sum _{i=1}^n(y^{(i)}-({\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}+b){)}^2$$

这就是平方误差之和（Sum of Squared Errors, SSE）。

MSE

通常，为了让损失函数的值不随样本数量变化而剧烈变化，我们将其除以样本数 n，得到均方误差（Mean Squared Error, MSE）：

$$\text{MSE}=\frac{1}{n}\sum _{i=1}^n(y^{(i)}-{\hat{y}}^{(i)}{)}^2$$

至此，我们完整地推导出了结论：在线性回归中，假设误差服从高斯分布，那么最大化数据似然性的过程，最终等价于最小化均方误差损失函数。

实践一下

让我们用代码来直观地感受这个过程。我们将创建一个带高斯噪声的线性数据集，然后用PyTorch的线性回归模型和MSE损失函数来拟合它。

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
 
# 1. 创建符合我们假设的数据集
# y = 2x + 1 + ε, 其中 ε ~ N(0, σ^2)
 
# 定义真实参数
true_w = torch.tensor([[2.0]])
true_b = torch.tensor([1.0])
num_samples = 100
 
# 生成特征 X
X = torch.randn(num_samples, 1) * 5
 
# 生成高斯噪声 ε
# 我们假设 σ=1.5
noise = torch.randn(num_samples, 1) * 1.5
 
# 生成真实标签 Y
# Y = X * w + b + noise
Y = X @ true_w + true_b + noise
 
print("Tensor Shapes:")
print(f"X shape: {X.shape}")
print(f"Y shape: {Y.shape}")
print("-" * 20)
 
# 2. 定义模型、损失函数和优化器
class LinearRegression(nn.Module):
    def __init__(self, input_dim, output_dim):
        super(LinearRegression, self).__init__()
        self.linear = nn.Linear(input_dim, output_dim)
 
    def forward(self, x):
        # x: [batch_size, input_dim]
        # output: [batch_size, output_dim]
        return self.linear(x)
 
# 模型配置
input_dim = 1
output_dim = 1
learning_rate = 0.01
epochs = 200
 
# 实例化
model = LinearRegression(input_dim, output_dim)
# 这里的 nn.MSELoss() 就是我们上面推导出的结果
# 它在内部计算 (prediction - target)^2 的均值
criterion = nn.MSELoss() 
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
 
# 3. 训练模型
# 这个训练循环的目标就是最小化MSE，也就是最大化我们数据的对数似然
for epoch in range(epochs):
    # 前向传播
    # y_pred shape: [num_samples, 1]
    y_pred = model(X)
    
    # 计算损失
    # loss是一个标量
    loss = criterion(y_pred, Y)
    
    # 反向传播和优化
    optimizer.zero_grad() # 清空梯度
    loss.backward()       # 计算梯度
    optimizer.step()      # 更新权重
 
    if (epoch + 1) % 20 == 0:
        print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}')
 
# 4. 结果可视化
print("\nTraining finished.")
print("Learned parameters:")
# model.parameters() 是一个生成器，我们可以把它转为列表查看
learned_params = list(model.parameters())
learned_w = learned_params[0]
learned_b = learned_params[1]
print(f"Learned w: {learned_w.item():.4f}, True w: {true_w.item():.4f}")
print(f"Learned b: {learned_b.item():.4f}, True b: {true_b.item():.4f}")
 
# 绘制结果
predicted = model(X).detach().numpy() # detach() 用于从计算图中分离张量
plt.figure(figsize=(10, 6))
plt.scatter(X.numpy(), Y.numpy(), label='Original data', alpha=0.7)
plt.plot(X.numpy(), predicted, color='r', label='Fitted line')
plt.title('Linear Regression with PyTorch')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()
 

这段代码中，我们创建了符合高斯噪声假设的数据，然后通过最小化nn.MSELoss，模型成功地学习到了接近真实的参数 w 和 b。

Tensor Shapes:
X shape: torch.Size([100, 1])
Y shape: torch.Size([100, 1])
--------------------
Epoch [20/200], Loss: 4.4227
Epoch [40/200], Loss: 3.3287
Epoch [60/200], Loss: 2.8263
Epoch [80/200], Loss: 2.5957
Epoch [100/200], Loss: 2.4898
Epoch [120/200], Loss: 2.4411
Epoch [140/200], Loss: 2.4188
Epoch [160/200], Loss: 2.4086
Epoch [180/200], Loss: 2.4039
Epoch [200/200], Loss: 2.4017
 
Training finished.
Learned parameters:
Learned w: 2.0855, True w: 2.0000
Learned b: 1.1513, True b: 1.0000

如果噪声是指数分布（拉普拉斯分布）呢？

我们刚才讨论了高斯噪声如何自然地导出均方误差（MSE，L2损失），现在我们来看看，如果噪声模型改变，损失函数会发生怎样有趣的变化。

在动手学深度学习这本书课后习题中，将我们的假设从“钟形”的高斯分布换成了一个在原点处更“尖锐”的拉普拉斯分布（Laplace distribution）。

拉普拉斯分布

设随机变量 $X$ 服从拉普拉斯分布，其概率密度函数（probability density function，PDF）为：

$$f(x|\mu ,b)=\frac{1}{2b}\exp \left(-\frac{|x-\mu |}{b}\right),-\infty <x<\infty$$

其中，$\mu$ 是位置参数（location parameter），决定了分布的中心位置，类似于正态分布中的均值，当 $x=\mu$ 时，概率密度函数取得最大值$\frac{1}{2b}$；$b$ 是尺度参数（scale parameter），且 $b>0$，$b$ 越大，分布越平坦，数据越分散，$b$ 越小，分布越集中 。

累积分布函数（cumulative distribution function，CDF）表示随机变量 $X$ 小于或等于 $x$ 的概率，记为 $F(x|\mu ,b)$，其表达式为：

$$F(x|\mu ,b)=\{\begin{array}{ll}\frac{1}{2}\exp \left(\frac{x-\mu }{b}\right),& x<\mu \\ 1-\frac{1}{2}\exp \left(-\frac{x-\mu }{b}\right),& x\ge \mu \end{array}$$

1. 负对数似然的推导 L1损失（MAE）

这个推导过程和我们之前对高斯噪声的分析路径完全一致，只是代入的概率密度函数不同。

第一步：写出单个样本的似然

我们的模型依然是 y = w^T*x + b + ε，因此误差项 ε = y - (w^T*x + b) = y - ŷ。

将这个误差代入拉普拉斯分布的概率密度函数中，我们就得到了在给定 x 和模型参数 w, b 的情况下，观测到 y 的概率（似然）：

$$P(y\mid \mathbf{x};\mathbf{w},b)=\frac{1}{2}\exp (-|y-({\mathbf{w}}^{\top }\mathbf{x}+b)|)$$

第二步：写出整个数据集的对数似然

根据最大似然估计（MLE），我们希望找到一组 w, b 来最大化所有独立样本的联合似然。同样，我们直接处理对数似然，将连乘变为连加：

$$\log L(\mathbf{w},b)=\log \left(\prod _{i=1}^{n}P(y^{(i)}\mid {\mathbf{x}}^{(i)};\mathbf{w},b)\right)$$ $$=\sum _{i=1}^n\log \left(\frac{1}{2}\exp (-|y^{(i)}-{\hat{y}}^{(i)}|)\right)$$

其中 ŷ^(i) = w^T*x^(i) + b。利用对数性质 log(A*B) = logA + logB 和 log(exp(x))=x：

$$=\sum _{i=1}^n\left(\log \left(\frac{1}{2}\right)+\log \left(\exp (-|y^{(i)}-{\hat{y}}^{(i)}|)\right)\right)$$ $$=\sum _{i=1}^n\left(-\log (2)-|y^{(i)}-{\hat{y}}^{(i)}|\right)$$ $$=-n\log (2)-\sum _{i=1}^n|y^{(i)}-{\hat{y}}^{(i)}|$$

第三步：转化为最小化问题（负对数似然）

机器学习的惯例是最小化损失函数。因此，我们将最大化对数似然，等价地转化为最小化负对数似然 -log L(w, b)：

$$\text{Loss}(\mathbf{w},b)=-\log L(\mathbf{w},b)=n\log (2)+\sum _{i=1}^n|y^{(i)}-{\hat{y}}^{(i)}|$$

在优化过程中，常数项 n log(2) 不影响最优解 w, b 的取值，因此可以被忽略。我们真正需要最小化的目标函数是：

$$\underset{\mathbf{w},b}{\mathrm{argmin}}\sum _{i=1}^n|y^{(i)}-{\hat{y}}^{(i)}|$$

这个形式我们非常熟悉，它就是绝对误差之和（Sum of Absolute Errors, SAE）。如果再除以样本数 n，就得到了平均绝对误差（Mean Absolute Error, MAE），也常被称为 L1 损失。

结论： 当线性回归模型的噪声被假设为服从拉普拉斯分布时，最大似然估计等价于最小化平均绝对误差（MAE） 损失函数。

2. 解析解的探讨

答案是：通常没有一个简单的、普适的解析解。

这与MSE的情况形成了鲜明对比。对于MSE，损失函数 Σ(y - ŷ)² 是一个处处可导的平滑凸函数。我们可以通过将其对 w 的偏导数置为零，得到一个线性方程组（即正规方程），从而直接解出 w。

但对于MAE，损失函数 Σ|y - ŷ| 包含绝对值函数。|z| 在 z=0 处是不可导的（有一个尖点）。这意味着当任何一个样本的预测值 ŷ^(i) 恰好等于真实值 y^(i) 时，损失函数在该点的梯度是未定义的。

由于损失函数并非处处可导，我们无法使用传统的求导置零的方法来获得一个简单的、封闭形式的解析解。这迫使我们必须使用迭代式的优化算法，比如梯度下降。

3. 随机梯度下降

算法描述

一个基本的SGD算法流程如下：

1. 随机初始化参数 w 和 b。
2. 在设定的训练轮数（epochs）内循环：
   1. 从数据集中随机抽取一个样本 (x^(i), y^(i))。
   2. 计算该样本的损失 L_i = |y^(i) - (w^T*x^(i) + b)|。
   3. 计算损失 L_i 关于 w 和 b 的梯度（或次梯度）。
   4. 沿着梯度的反方向更新参数： w ← w - η * ∇_w L_i b ← b - η * ∇_b L_i

梯度是什么？

L_i 对 w 的梯度计算需要用到链式法则。首先，我们需要 |z| 的导数，即符号函数 sgn(z)：

$$\frac{d|z|}{dz}=\text{sgn}(z)=\{\begin{array}{ll}1& \text{if }z>0\\ -1& \text{if }z<0\\ \text{undefined}& \text{if }z=0\end{array}$$

令 z = y^(i) - (w^T*x^(i) + b)，则 L_i = |z|。那么损失对权重 w_j (w的第j个分量) 的梯度为：

$${\nabla }_{w_j}{L}_i=\frac{\partial L_i}{\partial z}\frac{\partial z}{\partial w_j}=\text{sgn}(y^{(i)}-{\hat{y}}^{(i)})\cdot (-x_j^{(i)})$$

哪里会出错？（驻点附近的问题）

正如提示所说，问题出在驻点（y^(i) = ŷ^(i)）附近。

1. 梯度不连续性：当 ŷ^(i) 从略小于 y^(i) 变为略大于 y^(i) 时，sgn(...) 函数的值会从 +1 突变为 -1。这意味着梯度会瞬间反向，其大小并不会减小。
2. 梯度震荡（Oscillation）：想象一下，参数 w 已经非常接近最优解了。对于某个样本，ŷ^(i) 就在 y^(i) 附近来回摆动。当 ŷ^(i) < y^(i) 时，梯度是一个方向；一旦更新后 ŷ^(i) > y^(i)，梯度马上变成完全相反的方向。如果学习率 η 是固定的，更新的步长 η * |∇L| 不会随着接近最优解而减小，导致参数在最优解两侧“来回抖动”，难以精确收敛。

如何解决这个问题？

1. 次梯度（Subgradient）：对于 z=0 这个不可导的点，我们可以用“次梯度”来代替梯度。对于 f(z)=|z|，它在 z=0 的次梯度是 [-1, 1] 区间内的任意值。在实践中，我们通常简单地定义 sgn(0) = 0。这意味着，如果预测值恰好等于真实值，我们认为梯度为0，不进行更新。大多数深度学习框架（如PyTorch、TensorFlow）的 L1Loss 实现都隐式地处理了这一点。

2. 学习率衰减（Learning Rate Decay）：这是解决震荡问题最有效、最常用的方法。我们让学习率 η 随着训练的进行而逐渐减小。在训练初期，较大的学习率可以帮助参数快速接近最优区域；在训练后期，较小的学习率可以减小更新步长，抑制震荡，使得参数能够更稳定地收敛到最优解。

代码示例

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
 
# 1. 创建带拉普拉斯噪声的数据
# y = 3x - 2 + ε, 其中 ε 服从拉普拉斯分布
true_w = torch.tensor([[3.0]])
true_b = torch.tensor([-2.0])
num_samples = 200
 
X = torch.randn(num_samples, 1) * 2
# 生成拉普拉斯噪声 (scale=1)
laplace_dist = torch.distributions.laplace.Laplace(0, 1)
noise = laplace_dist.sample((num_samples, 1))
Y = X @ true_w + true_b + noise
 
# 2. 定义模型和L1损失函数
# 我们将手动实现SGD来更好地控制和观察
model = nn.Linear(1, 1)
criterion = nn.L1Loss() # 这就是PyTorch的MAE损失
 
# 3. 场景一：固定学习率
print("--- Scenario 1: Fixed Learning Rate ---")
torch.manual_seed(42) # for reproducibility
model_fixed_lr = nn.Linear(1, 1)
optimizer_fixed = torch.optim.SGD(model_fixed_lr.parameters(), lr=0.01)
fixed_lr_losses = []
 
for epoch in range(300):
    y_pred = model_fixed_lr(X)
    loss = criterion(y_pred, Y)
    optimizer_fixed.zero_grad()
    loss.backward()
    optimizer_fixed.step()
    fixed_lr_losses.append(loss.item())
    if (epoch + 1) % 50 == 0:
        print(f'Epoch [{epoch+1}/300], Loss: {loss.item():.4f}')
 
# 4. 场景二：衰减学习率
print("\n--- Scenario 2: Decaying Learning Rate ---")
torch.manual_seed(42)
model_decay_lr = nn.Linear(1, 1)
optimizer_decay = torch.optim.SGD(model_decay_lr.parameters(), lr=0.1) # 初始学习率可以大一些
# 每100个epoch，学习率乘以0.1
scheduler = torch.optim.lr_scheduler.StepLR(optimizer_decay, step_size=100, gamma=0.1)
decay_lr_losses = []
 
for epoch in range(300):
    y_pred = model_decay_lr(X)
    loss = criterion(y_pred, Y)
    optimizer_decay.zero_grad()
    loss.backward()
    optimizer_decay.step()
    scheduler.step() # 更新学习率
    decay_lr_losses.append(loss.item())
    if (epoch + 1) % 50 == 0:
        print(f'Epoch [{epoch+1}/300], Loss: {loss.item():.4f}, LR: {scheduler.get_last_lr()[0]:.4f}')
 
# 5. 结果可视化
plt.figure(figsize=(12, 6))
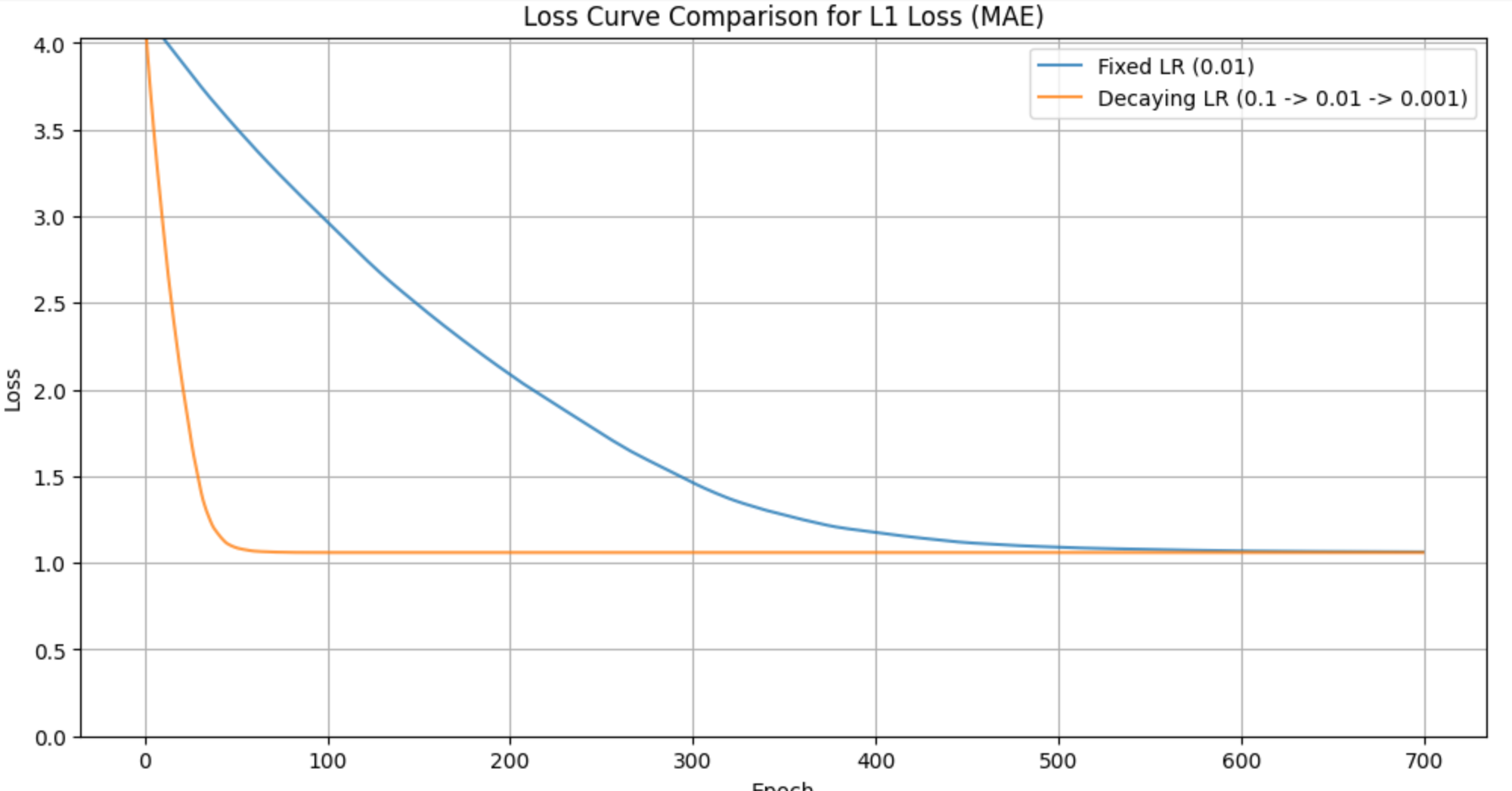
plt.plot(fixed_lr_losses, label='Fixed LR (0.01)', alpha=0.8)
plt.plot(decay_lr_losses, label='Decaying LR (0.1 -> 0.01 -> 0.001)', alpha=0.8)
plt.title('Loss Curve Comparison for L1 Loss (MAE)')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plt.grid(True)
plt.ylim(0, max(fixed_lr_losses[10], decay_lr_losses[10])) # 放大观察后期
plt.show()