主成分分析PCA-总体主成分分析

基本想法

这一节的核心是回答两个问题：我们为什么要做主成分分析？它究竟在做什么？

1. 解决“变量相关性”带来的分析难题

• 书中所述：“数据的变量之间可能存在相关性，以致增加了分析的难度。”
• 假设一个数据集，记录了中学生的身高（厘米）、体重（公斤）和立定跳远成绩（米）。这三个变量很可能不是独立的。身高越高、体重越重的学生，可能跳得更远（也可能跳不远，但它们之间存在某种关系）。如果我们直接用这三个相关的变量去建模，信息是有冗余的。比如，身高和体重可能共同反映了一个更本质的特征，不妨称之为“身体素质”。
• PCA的目标：我们希望能找到一个新的变量，比如就叫“身体素质综合得分”（$y_1$），它是一个由身高、体重、跳远成绩线性组合而成的新变量。这个新变量应该尽可能多地包含原来三个变量中的信息。如果一个新变量不够，我们就找第二个、第三个，但要求这些新变量之间互相独立、没有冗余信息。这就是书中所说的“由少数不相关的变量来代替相关的变量”。

2. 坐标系旋转与最大方差

在《机器学习方法》中，李航老师用了一个非常精彩的类比：“主成分分析等价于进行坐标系旋转变换”。

• 原始数据：假设一下二维平面上有一堆散点，代表了学生的（身高，体重）数据。这些点可能呈一个斜向上的椭圆形分布，这正体现了身高和体重的相关性。我们用原始的坐标轴（身高轴，体重轴）来描述这些点。

• PCA要做什么？ PCA不改变数据点本身，而是试图找到一个新的坐标系来更好地描述这堆数据。

  • 寻找新坐标轴 (主成分)：
    1. 第一主成分 ($y_1$)：寻找一个新的坐标轴方向，当我们把所有数据点都投影到这个新轴上时，这些投影点的方差最大。在我们的例子里，这个新轴的方向大致就是椭圆的长轴方向。为什么是方差最大？因为方差衡量了数据的离散程度。方差最大的方向，就是数据变化最剧烈、包含信息最丰富的方向。
    2. 第二主成分 ($y_2$)：寻找第二个坐标轴方向。这个方向必须与第一个坐标轴正交（垂直），并且在所有与第一主成分正交的方向中，它同样使得数据投影后的方差最大。在我们的例子里，这基本就是椭圆的短轴方向。
    3. 以此类推，直到找到m个新的坐标轴。

• “信息保持”与“降维”

  • 信息保持：书中提到“要求能够保留数据中的大部分信息”。在PCA的语境下，“信息”由方差来度量。所有新坐标轴上的方差之和，等于原始坐标轴上的方差之和。这意味着坐标旋转本身没有丢失任何信息。
  • 降维：但我们发现，第一个主成分（椭圆长轴）方向上的方差远大于第二个主成分（椭圆短轴）方向上的方差。这意味着，如果我们只保留第一主成分，用一个一维的“身体素质综合得分”来代替二维的（身高，体重），我们可能已经保留了原始数据95%的信息。这就是降维。

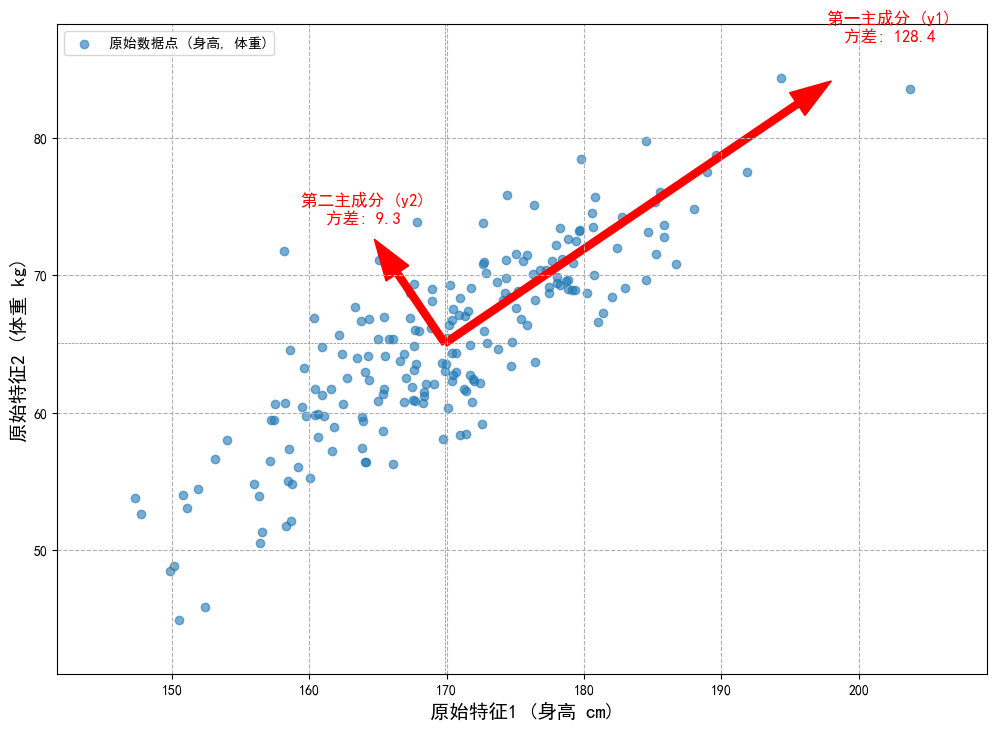
PCA的本质，是通过正交变换（坐标系旋转），将一组可能相关的原始变量，转化为一组线性无关的新变量（主成分）。这些新变量按照方差从大到小排列，使得我们可以用方差最大的前几个新变量来近似代表整个数据集，从而达到降维和去相关的目的。

---

定义和导出 (The “How”, in Math)

现在，我们把上面这些直观的想法，用精确的数学语言来描述。这就是书中16.1.2节的核心任务。

1. 数学设定

• 随机向量 $\mathbf{x}$:

  $$\mathbf{x}=(x_1,x_2,\dots ,x_m{)}^T$$

  这不再是具体的数据点了，而是代表一个包含 $m$ 个随机变量的向量。比如，$\mathbf{x}$ 可以是（身高, 体重, 跳远成绩）这三个随机变量的集合。

• 均值向量 $\mu$:

  $$\mu =E(\mathbf{x})=({\mu }_1,{\mu }_2,\dots ,{\mu }_m{)}^T$$

  这是随机向量 $\mathbf{x}$ 的期望值，包含了每个变量的平均值。

• 协方差矩阵 $\mathbf{\Sigma }$:

  $$\mathbf{\Sigma }=\text{cov}(\mathbf{x},\mathbf{x})=E[(\mathbf{x}-\mu )(\mathbf{x}-\mu {)}^T]$$

  这是至关重要的概念。这是一个 $m\times m$ 的对称矩阵。

  • 对角线元素 ${\Sigma }_{ii}$ 是第 $i$ 个变量自身的方差，即 $\text{var}(x_i)$。
  • 非对角线元素 ${\Sigma }_{ij}$ 是第 $i$ 和第 $j$ 个变量的协方差，即 $\text{cov}(x_i,x_j)$。
  • 协方差矩阵完美地描述了原始变量间的相关性。==我们的目标就是通过一个变换，得到一组新变量，使得它们的新协方差矩阵变成一个对角矩阵（即非对角线元素全为0，表示新变量间线性无关）。==

2. 线性变换

我们寻找的新变量 $y_i$ 是原始变量 $x_j$ 的线性组合。

$$y_i={\alpha }_{i1}{x}_1+{\alpha }_{i2}{x}_2+\cdots +{\alpha }_{im}{x}_m$$

写成向量形式就是：

$$y_i={\alpha }_i^T\mathbf{x}$$

• $\mathbf{x}$: 原始的 $m$ 维随机向量。
• ${\alpha }_i=({\alpha }_{i1},{\alpha }_{i2},\dots ,{\alpha }_{im}{)}^T$: 这是一个 $m$ 维的系数向量或权重向量。它定义了一个方向。PCA的核心任务，就是要找到这一组最佳的 ${\alpha }_i$。
• $y_i$: 变换后的新变量，是一个标量。它就是 $\mathbf{x}$ 在 ${\alpha }_i$ 方向上的投影（如果 ${\alpha }_i$ 是单位向量）。

3. 新变量的统计性质

一旦定义了变换 $y_i={\alpha }_i^T\mathbf{x}$，利用随机变量的性质，我们可以马上推导出新变量的期望、方差和协方差：

• 期望 (式16.2):

  $$E(y_i)=E({\alpha }_i^T\mathbf{x})={\alpha }_i^{T}E(\mathbf{x})={\alpha }_i^T\mu$$

  (因为期望是线性运算)

• 方差 (式16.3):

  $$\text{var}(y_i)=\text{cov}(y_i,y_i)=\text{cov}({\alpha }_i^T\mathbf{x},{\alpha }_i^T\mathbf{x})={\alpha }_i^T\text{cov}(\mathbf{x},\mathbf{x}){\alpha }_i={\alpha }_i^T\mathbf{\Sigma }{\alpha }_i$$

  ==这个公式是核心中的核心。它告诉我们，新变量的方差，完全由原始数据的协方差矩阵 $\mathbf{\Sigma }$ 和我们选择的方向 ${\alpha }_i$ 决定。 我们的目标就是最大化这个值！==

• 协方差 (式16.4):

  $$\text{cov}(y_i,y_j)={\alpha }_i^T\mathbf{\Sigma }{\alpha }_j$$

  这个公式衡量了任意两个新变量 $y_i$ 和 $y_j$ 之间的相关性。==我们的目标就是让这个值在 $i\ne j$ 时等于0！==

4. 定义16.1 (总体主成分)

这个定义将我们前面所有的直观想法和数学推导，总结成了三条严格的规则。这三条规则合在一起，就构成了一个带约束的序贯优化问题。

• 条件(1): ${\alpha }_i^T{\alpha }_i=1$

  • 数学意义: 系数向量 ${\alpha }_i$ 是单位向量，它的长度为1。
  • 为什么需要这个条件? 如果没有这个约束，我们可以通过单纯地把 ${\alpha }_i$ 的所有元素乘以100，来让方差 $\text{var}(y_i)={\alpha }_i^T\mathbf{\Sigma }{\alpha }_i$ 变成原来的10000倍。这样最大化方差就没意义了。这个条件确保我们只关心方向，而不是向量的长度。

• 条件(2): $y_i$ 与 $y_j$ 互不相关，即 $\text{cov}(y_i,y_j)=0(i\ne j)$

  • 数学意义: 根据式(16.4)，这就等价于 ${\alpha }_i^T\mathbf{\Sigma }{\alpha }_j=0(i\ne j)$。
  • 直观联系: 这就是我们“新坐标轴要正交”这个思想在统计上的体现。注意，这里的正交是“关于 $\mathbf{\Sigma }$ 的正交”，它保证了新变量在统计意义上的线性无关。

• 条件(3): $y_1$ 方差最大，$y_2$ 是与 $y_1$ 无关的方差最大者，以此类推。

  • 这是一个逐级寻找（贪心）的过程:

    1. 求第一主成分 $y_1$: 我们要求解的优化问题是：

       $$\underset{{\alpha }_1}{\max }{\alpha }_1^T\mathbf{\Sigma }{\alpha }_1\text{s.t.}{\alpha }_1^T{\alpha }_1=1$$

    2. 求第二主成分 $y_2$: 在所有与 $y_1$ 不相关的线性变换中，找方差最大的。优化问题是：

       $$\underset{{\alpha }_2}{\max }{\alpha }_2^T\mathbf{\Sigma }{\alpha }_2\text{s.t.}{\alpha }_2^T{\alpha }_2=1\text{and}\text{cov}(y_1,y_2)={\alpha }_1^T\mathbf{\Sigma }{\alpha }_2=0$$

    3. 求第 $k$ 主成分 $y_k$: 以此类推。

---

至此，“问题是什么” 已经定义得非常清楚了。接下来的内容，就是去 “如何求解” 这个优化问题了。而这个求解过程，将不可避免地与协方差矩阵 $\mathbf{\Sigma }$ 的特征值分解联系在一起。

---

核心：定理16.1 的证明

定理 16.1

设 $\mathbf{x}$ 是 $m$ 维随机变量，$\mathbf{\Sigma }$ 是 $\mathbf{x}$ 的协方差矩阵，$\mathbf{\Sigma }$ 的特征值分别是 ${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_m\ge 0$，特征值对应的单位特征向量分别是 ${\mathbf{\alpha }}_1,{\mathbf{\alpha }}_2,\cdots ,{\mathbf{\alpha }}_m$，则 $\mathbf{x}$ 的第 $k$ 主成分是

$y_k={\mathbf{\alpha }}_k^T\mathbf{x}={\alpha }_{1k}{x}_1+{\alpha }_{2k}{x}_2+\cdots +{\alpha }_{mk}{x}_m,k=1,2,\cdots ,m$

$\mathbf{x}$ 的第 $k$ 主成分的方差是

$\text{var}(y_k)={\mathbf{\alpha }}_k^T\mathbf{\Sigma }{\mathbf{\alpha }}_k={\lambda }_k,k=1,2,\cdots ,m$

即协方差矩阵 $\mathbf{\Sigma }$ 的第 $k$ 个特征值。

定理内容简述: 这个定理告诉我们一个惊人的结论：==我们费尽心思定义的、通过“序贯最大化方差”得到的主成分，其方向向量 ${\alpha }_k$ 恰好就是协方差矩阵 $\mathbf{\Sigma }$ 的特征向量，而该主成分的方差 $\text{var}(y_k)$ 恰好就是对应的特征值 ${\lambda }_k$。==

这个定理把一个复杂的优化问题，转化成了一个我们非常熟悉的线性代数问题——求解矩阵的特征值和特征向量。

---

第一步：证明第一主成分

我们的目标是求解下面这个带约束的优化问题：

$$\underset{{\alpha }_1}{\max }{\alpha }_1^T\mathbf{\Sigma }{\alpha }_1\text{s.t.}{\alpha }_1^T{\alpha }_1=1$$

1. 构造拉格朗日函数 (Why Lagrange Multipliers?)

• 回顾：拉格朗日乘子法是解决“带等式约束的优化问题”的标准工具。它的核心思想是，将约束条件乘以一个拉格朗日乘子（比如 $\lambda$），然后从目标函数中减去它，从而构造一个新的、无约束的拉格朗日函数。通过对这个新函数求导并令其为0，我们就能找到原问题的可能极值点。

• 我们的问题:

  • 目标函数: $f({\alpha }_1)={\alpha }_1^T\mathbf{\Sigma }{\alpha }_1$
  • 等式约束: $g({\alpha }_1)={\alpha }_1^T{\alpha }_1-1=0$

• 构造拉格朗日函数 $L({\alpha }_1,\lambda )$:

  $$L({\alpha }_1,\lambda )=f({\alpha }_1)-\lambda g({\alpha }_1)={\alpha }_1^T\mathbf{\Sigma }{\alpha }_1-\lambda ({\alpha }_1^T{\alpha }_1-1)$$

2. 对 ${\alpha }_1$ 求导并令其为0 (The Calculus)

现在，我们将 $L({\alpha }_1,\lambda )$ 看作是关于变量 ${\alpha }_1$ 的函数，并对它求梯度。这里需要用到两个矩阵求导的常用公式：

• $\frac{\partial ({\mathbf{x}}^T\mathbf{Ax})}{\partial \mathbf{x}}=2\mathbf{Ax}$ (当 $\mathbf{A}$ 是对称矩阵时，而在我们本次求解中 $\mathbf{\Sigma }$ 就是对称的)

• $\frac{\partial ({\mathbf{x}}^T\mathbf{x})}{\partial \mathbf{x}}=2\mathbf{x}$

• 求导过程:

  $$\begin{array}{rlrl}\frac{\partial L}{\partial {\alpha }_1}& =\frac{\partial }{\partial {\alpha }_1}\left({\alpha }_1^T\mathbf{\Sigma }{\alpha }_1-\lambda ({\alpha }_1^T{\alpha }_1-1)\right)& & \\ & =\frac{\partial ({\alpha }_1^T\mathbf{\Sigma }{\alpha }_1)}{\partial {\alpha }_1}-\lambda \frac{\partial ({\alpha }_1^T{\alpha }_1)}{\partial {\alpha }_1}-\frac{\partial (-\lambda )}{\partial {\alpha }_1}& & \text{（对各项求导）}\\ & =2\mathbf{\Sigma }{\alpha }_1-\lambda (2{\alpha }_1)-0& & \text{（应用矩阵求导公式）}\\ & =2(\mathbf{\Sigma }{\alpha }_1-\lambda {\alpha }_1)& & \end{array}$$

• 令导数为0:

  $$\begin{gathered} 2(\mathbf{\Sigma }{\alpha }_1-\lambda {\alpha }_1)=0 \\ ⟹\mathbf{\Sigma }{\alpha }_1=\lambda {\alpha }_1 \end{gathered}$$

3. 解读结果

$\mathbf{\Sigma }{\alpha }_1=\lambda {\alpha }_1$ 这个方程眼熟吗？这不就是线性代数中特征值和特征向量的定义！

• $\lambda$ 是协方差矩阵 $\mathbf{\Sigma }$ 的一个特征值。
• ${\alpha }_1$ 是与该特征值 $\lambda$ 对应的特征向量。

我们还没结束。我们要求的是目标函数 ${\alpha }_1^T\mathbf{\Sigma }{\alpha }_1$ 的最大值。我们来看看这个最大值是什么：

$$\begin{array}{rlrl}\text{var}(y_1)& ={\alpha }_1^T\mathbf{\Sigma }{\alpha }_1& & \text{（目标函数）}\\ & ={\alpha }_1^T(\mathbf{\Sigma }{\alpha }_1)& & \text{（矩阵乘法结合律）}\\ & ={\alpha }_1^T(\lambda {\alpha }_1)& & \text{（因为 Σα1=λα1）}\\ & =\lambda ({\alpha }_1^T{\alpha }_1)& & \text{（提出标量 λ）}\\ & =\lambda \cdot 1& & \text{（根据约束条件 α1Tα1=1）}\\ & =\lambda & & \end{array}$$

这说明，目标函数的值（也就是第一主成分的方差）就等于特征值 $\lambda$。为了让这个方差最大化，我们显然应该选择最大的那个特征值，我们称之为 ${\lambda }_1$。

妙！第一主成分 $y_1={\alpha }_1^T\mathbf{x}$ 的系数向量 ${\alpha }_1$ 是协方差矩阵 $\mathbf{\Sigma }$ 的最大特征值 ${\lambda }_1$ 所对应的单位特征向量。第一主成分的方差就是 ${\lambda }_1$。

---

第二步：证明第二主成分

现在的问题变得更复杂了，我们有两个约束条件：

$$\underset{{\alpha }_2}{\max }{\alpha }_2^T\mathbf{\Sigma }{\alpha }_2$$ $$\text{s.t.}\{\begin{array}{ll}{\alpha }_2^T{\alpha }_2=1& \text{(约束1: 单位向量)}\\ \text{cov}(y_1,y_2)={\alpha }_1^T\mathbf{\Sigma }{\alpha }_2=0& \text{(约束2: 与第一主成分无关)}\end{array}$$

1. 简化约束2 (The Trick)

李航老师在书中用了一个非常巧妙的简化。让我们看看约束2：${\alpha }_1^T\mathbf{\Sigma }{\alpha }_2=0$。

因为我们已经知道 ${\alpha }_1$ 是 $\mathbf{\Sigma }$ 关于 ${\lambda }_1$ 的特征向量，所以 $\mathbf{\Sigma }{\alpha }_1={\lambda }_1{\alpha }_1$。由于 $\mathbf{\Sigma }$ 是对称矩阵，它的转置等于自身 (${\mathbf{\Sigma }}^T=\mathbf{\Sigma }$)。所以，我们可以对 $\mathbf{\Sigma }{\alpha }_1={\lambda }_1{\alpha }_1$ 两边同时取转置： $(\mathbf{\Sigma }{\alpha }_1{)}^T=({\lambda }_1{\alpha }_1{)}^T⟹{\alpha }_1^T{\mathbf{\Sigma }}^T={\lambda }_1{\alpha }_1^T⟹{\alpha }_1^T\mathbf{\Sigma }={\lambda }_1{\alpha }_1^T$。

现在把这个代入约束2：

$${\alpha }_1^T\mathbf{\Sigma }{\alpha }_2=({\lambda }_1{\alpha }_1^T){\alpha }_2={\lambda }_1({\alpha }_1^T{\alpha }_2)=0$$

由于 ${\lambda }_1$ 是最大特征值（通常大于0，除非数据完全没有变化），所以上式成立的唯一可能是：

$${\alpha }_1^T{\alpha }_2=0$$

这意味着，“新变量 $y_1$ 和 $y_2$ 线性无关”这个统计条件，等价于“方向向量 ${\alpha }_1$ 和 ${\alpha }_2$ 几何正交”这个几何条件！

这极大地简化了问题！李航老师在书中直接使用了这个正交条件，但这是背后的推导。

2. 构造新的拉格朗日函数

现在我们的优化问题是：

$$\underset{{\alpha }_2}{\max }{\alpha }_2^T\mathbf{\Sigma }{\alpha }_2\text{s.t.}{\alpha }_2^T{\alpha }_2=1\text{and}{\alpha }_1^T{\alpha }_2=0$$

我们有两个约束，所以需要两个拉格朗日乘子，$\lambda$ 和 $\varphi$。

$$L({\alpha }_2,\lambda ,\varphi )={\alpha }_2^T\mathbf{\Sigma }{\alpha }_2-\lambda ({\alpha }_2^T{\alpha }_2-1)-\varphi ({\alpha }_1^T{\alpha }_2)$$

3. 对 ${\alpha }_2$ 求导并令其为0

$$\frac{\partial L}{\partial {\alpha }_2}=\mathbf{\Sigma }{\alpha }_2-\lambda {\alpha }_2-\varphi {\alpha }_1=0$$

**4. 消去乘子 $\varphi$

这个方程里有我们不想要的 $\varphi$。如何消掉它？我们可以利用向量的正交性。 用 ${\alpha }_1^T$ 左乘上式两端：

$${\alpha }_1^T(\mathbf{\Sigma }{\alpha }_2-\lambda {\alpha }_2-\varphi {\alpha }_1)={\alpha }_1^{T}0$$ $${\alpha }_1^T\mathbf{\Sigma }{\alpha }_2-\lambda {\alpha }_1^T{\alpha }_2-\varphi {\alpha }_1^T{\alpha }_1=0$$

现在我们来分析这一长串式子的每一项：

• ${\alpha }_1^T\mathbf{\Sigma }{\alpha }_2$: 根据我们的约束条件，这一项为 $0$。
• $\lambda {\alpha }_1^T{\alpha }_2$: 根据我们推导出的简化约束，${\alpha }_1^T{\alpha }_2=0$，所以这一项也为 $0$。
• $\varphi {\alpha }_1^T{\alpha }_1$: 因为 ${\alpha }_1$ 是单位向量，所以 ${\alpha }_1^T{\alpha }_1=1$。

代入回去，我们得到：

$$(0)-\lambda (0)-\varphi (1)=0⟹-\varphi =0⟹\varphi =0$$

这真是一个漂亮的结果！这意味着第二个拉格朗日乘子 $\varphi$ 必须是0。

现在把 $\varphi =0$ 代回到求导后的方程 $\mathbf{\Sigma }{\alpha }_2-\lambda {\alpha }_2-\varphi {\alpha }_1=0$ 中，得到：

$$\mathbf{\Sigma }{\alpha }_2-2\lambda {\alpha }_2=0⟹\mathbf{\Sigma }{\alpha }_2=\lambda {\alpha }_2$$

5. 看看结果

这和我们对第一主成分的推导结果形式完全一样！它表明，${\alpha }_2$ 也必须是 $\mathbf{\Sigma }$ 的一个特征向量。

但是是哪个呢？我们的目标是最大化方差 $\text{var}(y_2)={\alpha }_2^T\mathbf{\Sigma }{\alpha }_2=\lambda$。由于我们已经用掉了最大的特征值 ${\lambda }_1$ 给了第一主成分，并且 ${\alpha }_2$ 必须与 ${\alpha }_1$ 正交，所以我们只能在剩下的特征值中选择最大的一个。

因为对称矩阵的属于不同特征值的特征向量是天然正交的，所以我们选择的 ${\alpha }_2$ 自动满足与 ${\alpha }_1$ 正交的条件。因此，我们应该选择第二大的特征值 ${\lambda }_2$。

所以！第二主成分 $y_2={\alpha }_2^T\mathbf{x}$ 的系数向量 ${\alpha }_2$ 是协方差矩阵 $\mathbf{\Sigma }$ 的第二大特征值 ${\lambda }_2$ 所对应的单位特征向量。第二主成分的方差就是 ${\lambda }_2$。

---

第三步：推广到第 k 主成分

通过数学归纳法，我们可以将这个逻辑推广下去。 假设我们已经求出了前 $k-1$ 个主成分，它们的系数向量是 ${\alpha }_1,\dots ,{\alpha }_{k-1}$，对应 $\mathbf{\Sigma }$ 的前 $k-1$ 大的特征值 ${\lambda }_1,\dots ,{\lambda }_{k-1}$。

要求第 $k$ 主成分，优化问题是：

$$\underset{{\alpha }_k}{\max }{\alpha }_k^T\mathbf{\Sigma }{\alpha }_k$$ $$\text{s.t.}{\alpha }_k^T{\alpha }_k=1\text{and}{\alpha }_i^T{\alpha }_k=0,\text{for }i=1,\dots ,k-1$$

用同样的方法构造拉格朗日函数，会发现最优解 ${\alpha }_k$ 必须是 $\mathbf{\Sigma }$ 的第 $k$ 大的特征值 ${\lambda }_k$ 所对应的单位特征向量。

至此，定理16.1 证毕。

---

推论 16.1 和主要性质

定理证明之后，剩下的性质就都是这个核心结论的自然推论了。

推论 16.1 与 矩阵形式

推论 16.1

$m$ 维随机变量 $\mathbf{y}=(y_1,y_2,\cdots ,y_m{)}^T$ 的分量依次是 $\mathbf{x}$ 的第一主成分到第 $m$ 主成分的充要条件是：

1. $\mathbf{y}={\mathbf{A}}^T\mathbf{x}$，$\mathbf{A}$ 为正交矩阵：

$$\mathbf{A}=\left[\begin{array}{cccc}{\alpha }_{11}& {\alpha }_{12}& \cdots & {\alpha }_{1m}\\ {\alpha }_{21}& {\alpha }_{22}& \cdots & {\alpha }_{2m}\\ ⋮& ⋮& & ⋮\\ {\alpha }_{m1}& {\alpha }_{m2}& \cdots & {\alpha }_{mm}\end{array}\right]$$

2. $\mathbf{y}$ 的协方差矩阵为对角矩阵：

$$\text{cov}(\mathbf{y})=\text{diag}({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_m)$$ $${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_m$$

其中，${\lambda }_k$ 是 $\mathbf{\Sigma }$ 的第 $k$ 个特征值，${\mathbf{\alpha }}_k$ 是对应的单位特征向量，$k=1,2,\cdots ,m$。

• (1) $y={\mathbf{A}}^T\mathbf{x}$: 这只是把所有 $m$ 个线性变换 $y_k={\alpha }_k^T\mathbf{x}$ 写成了矩阵形式。

  • $\mathbf{A}$ 是一个 $m\times m$ 的矩阵，它的每一列是我们的主成分方向向量 ${\alpha }_k$。
  $$\mathbf{A}=[{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_m]$$
  • 因为所有的 ${\alpha }_k$ 都是单位向量且相互正交，所以 $\mathbf{A}$ 是一个正交矩阵。正交矩阵有一个极好的性质：${\mathbf{A}}^T\mathbf{A}=\mathbf{A}{\mathbf{A}}^T=\mathbf{I}$ (单位矩阵)。

• (2) $y$ 的协方差矩阵是对角矩阵 我们来推导新变量向量 $\mathbf{y}$ 的协方差矩阵：

  $$\begin{array}{rlrl}\text{cov}(\mathbf{y})& =E[(\mathbf{y}-E[\mathbf{y}])(\mathbf{y}-E[\mathbf{y}]{)}^T]& & \\ & =E[({\mathbf{A}}^T\mathbf{x}-E[{\mathbf{A}}^T\mathbf{x}])({\mathbf{A}}^T\mathbf{x}-E[{\mathbf{A}}^T\mathbf{x}]{)}^T]& & \\ & =E[{\mathbf{A}}^T(\mathbf{x}-E[\mathbf{x}])({\mathbf{A}}^T(\mathbf{x}-E[\mathbf{x}]){)}^T]& & \\ & =E[{\mathbf{A}}^T(\mathbf{x}-\mu )(\mathbf{x}-\mu {)}^T\mathbf{A}]& & \\ & ={\mathbf{A}}^{T}E[(\mathbf{x}-\mu )(\mathbf{x}-\mu {)}^T]\mathbf{A}& & \text{（A是常数矩阵，可提出期望）}\\ & ={\mathbf{A}}^T\mathbf{\Sigma A}& & \end{array}$$

  这就是新协方差矩阵的表达式。我们知道 $\mathbf{\Sigma A}=\mathbf{\Sigma }[{\alpha }_1,\dots ,{\alpha }_m]=[\mathbf{\Sigma }{\alpha }_1,\dots ,\mathbf{\Sigma }{\alpha }_m]=[{\lambda }_1{\alpha }_1,\dots ,{\lambda }_m{\alpha }_m]=\mathbf{A\Lambda }$，其中 $\mathbf{\Lambda }$ 是一个对角线上元素为 ${\lambda }_1,\dots ,{\lambda }_m$ 的对角矩阵。 所以：

  $$\text{cov}(\mathbf{y})={\mathbf{A}}^T\mathbf{\Sigma A}={\mathbf{A}}^T(\mathbf{A\Lambda })=({\mathbf{A}}^T\mathbf{A})\mathbf{\Lambda }=\mathbf{I\Lambda }=\mathbf{\Lambda }$$ $$\mathbf{\Lambda }=\text{diag}({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_m)$$

  这完美地证明了，经过PCA变换后，新变量的协方差矩阵是一个对角矩阵，对角元就是原始协方差矩阵的特征值。这在数学上证明了新变量之间是线性无关的。

性质 (1) & (2): 总方差不变性

• 性质(1) 就是我们刚才证明的结论：$\text{cov}(\mathbf{y})=\mathbf{\Lambda }$。
• 性质(2) $\sum {\lambda }_i=\sum {\sigma }_{ii}$ 这个性质说明，变换前后的总方差保持不变。PCA只是将总方差进行了重新分配，将它集中到了前几个主成分上。

  • 证明: 利用了矩阵的迹（trace，对角线元素之和）的性质：$\text{tr}(\mathbf{AB})=\text{tr}(\mathbf{BA})$。

    $$\begin{array}{rlrl}\sum _{i=1}^m\text{var}(x_i)& =\sum _{i=1}^m{\sigma }_{ii}=\text{tr}(\mathbf{\Sigma })& & \text{（总方差是协方差矩阵的迹）}\\ \text{而我们有 }\mathbf{\Sigma }& =\mathbf{A\Lambda }{\mathbf{A}}^T(\text{这被称为特征值分解})& & \\ \text{tr}(\mathbf{\Sigma })& =\text{tr}(\mathbf{A\Lambda }{\mathbf{A}}^T)& & \\ & =\text{tr}({\mathbf{A}}^T\mathbf{A\Lambda })& & \text{（利用迹的性质 tr(BC) = tr(CB), B=A, C=ΛAᵀ）}\\ & =\text{tr}(\mathbf{I\Lambda })& & \text{（因为 A 是正交矩阵）}\\ & =\text{tr}(\mathbf{\Lambda })& & \\ & =\sum _{i=1}^m{\lambda }_i=\sum _{i=1}^m\text{var}(y_i)& & \end{array}$$
  证明完毕。

性质(3), (4), (5): 因子负荷量 (Factor Loadings)

这部分是解释主成分的物理意义。因子负荷量 $\rho (y_k,x_i)$ 衡量的是第k个主成分 $y_k$ 与原始的某个变量 $x_i$ 之间的相关系数。它的绝对值越大，说明 $y_k$ 主要由这个 $x_i$ 解释。

• 推导式(16.20):
  • 相关系数定义: $\rho (A,B)=\frac{\text{cov}(A,B)}{\sqrt{\text{var}(A)\text{var}(B)}}$
  • 代入:
    • $\text{var}(y_k)={\lambda }_k$ (我们已证)
    • $\text{var}(x_i)={\sigma }_{ii}$ (定义)
    • 关键是算分子 $\text{cov}(y_k,x_i)$:
      • $x_i$ 可以表示为 ${\mathbf{e}}_i^T\mathbf{x}$，其中 ${\mathbf{e}}_i$ 是一个标准基向量（第i个元素是1，其余是0）。
      • $\text{cov}(y_k,x_i)=\text{cov}({\alpha }_k^T\mathbf{x},{\mathbf{e}}_i^T\mathbf{x})={\alpha }_k^T\mathbf{\Sigma }{\mathbf{e}}_i$
      • 因为 $\mathbf{\Sigma }{\alpha }_k={\lambda }_k{\alpha }_k$, 两边取转置得到 ${\alpha }_k^T\mathbf{\Sigma }={\lambda }_k{\alpha }_k^T$.
      • 所以 $\text{cov}(y_k,x_i)=({\lambda }_k{\alpha }_k^T){\mathbf{e}}_i={\lambda }_k({\alpha }_k^T{\mathbf{e}}_i)={\lambda }_k{\alpha }_{ik}$ (其中 ${\alpha }_{ik}$ 是向量 ${\alpha }_k$ 的第 $i$ 个分量)。
  • 组合起来:

因子负荷量

$$\rho (y_k,x_i)=\frac{{\lambda }_k{\alpha }_{ik}}{\sqrt{{\lambda }_k{\sigma }_{ii}}}=\frac{\sqrt{{\lambda }_k}{\alpha }_{ik}}{\sqrt{{\sigma }_{ii}}}$$

• 性质(4)：第k个主成分与所有原始变量的相关系数的平方和，等于其方差（特征值）。这是对主成分“能量”的另一种解释。

  • 证明:

    $$\sum _{i=1}^m{\sigma }_{ii}{\rho }^2(y_k,x_i)=\sum _{i=1}^m{\sigma }_{ii}{\left(\frac{\sqrt{{\lambda }_k}{\alpha }_{ik}}{\sqrt{{\sigma }_{ii}}}\right)}^2=\sum _{i=1}^m{\sigma }_{ii}\frac{{\lambda }_k{\alpha }_{ik}^2}{{\sigma }_{ii}}=\sum _{i=1}^m{\lambda }_k{\alpha }_{ik}^2={\lambda }_k\sum _{i=1}^m{\alpha }_{ik}^2$$

    因为 ${\alpha }_k=({\alpha }_{1k},\dots ,{\alpha }_{mk}{)}^T$ 是单位向量，所以它的各分量平方和 ${\sum }_i{\alpha }_{ik}^2={\alpha }_k^T{\alpha }_k=1$。 因此，上式等于 ${\lambda }_k\cdot 1={\lambda }_k$。得证。

• 性质(5)：某个原始变量与所有主成分的相关系数的平方和为1（假设该变量已标准化）。这说明所有主成分一起，可以完全解释原始变量的方差。

---

主成分的个数

这一小节的根本目的，是为我们进行主成分分析的核心目标——降维。它旨在证明：当我们决定只保留 $q$ 个新变量来近似原始数据时，选择前 $q$ 个主成分是保留信息（即方差）的最优策略。这个结论由 定理16.2 给出。

定理 16.2

定理 16.2

对任意正整数 $q$, $1\le q\le m$，考虑从 $m$ 维随机变量 $\mathbf{x}$ 到 $q$ 维随机变量 $\mathbf{y}$ 的任意正交线性变换

$$\mathbf{y}={\mathbf{B}}^T\mathbf{x}$$

其中，$\mathbf{B}$ 是一个 $m\times q$ 矩阵，其列向量是标准正交的（即 ${\mathbf{B}}^T\mathbf{B}={\mathbf{I}}_q$）。变换后变量 $\mathbf{y}$ 的协方差矩阵为

$${\mathbf{\Sigma }}_{\mathbf{y}}={\mathbf{B}}^T\mathbf{\Sigma B}$$

则 ${\mathbf{\Sigma }}_{\mathbf{y}}$ 的迹 $\text{tr}({\mathbf{\Sigma }}_{\mathbf{y}})$ 在 $\mathbf{B}={\mathbf{A}}_q$ 时取得最大值。这里的 ${\mathbf{A}}_q=[{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_q]$ 是由协方差矩阵 $\mathbf{\Sigma }$ 的前 $q$ 个特征向量（对应前 $q$ 大的特征值）构成的矩阵。

---

定理 16.2 的证明

我们的目标: 求解以下优化问题：

$$\underset{\mathbf{B}}{\max }\text{tr}({\mathbf{B}}^T\mathbf{\Sigma B})\text{s.t.}{\mathbf{B}}^T\mathbf{B}={\mathbf{I}}_q$$

这里的 $\text{tr}({\mathbf{\Sigma }}_{\mathbf{y}})$ 是新变量 $y_1,\dots ,y_q$ 的方差之和，代表了变换后数据所保留的总方差。

第一步：基变换——用主成分基底表示B

这是证明中最精妙的一步。我们知道，由协方差矩阵 $\mathbf{\Sigma }$ 的 $m$ 个标准正交特征向量 $\{{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_m\}$ 构成的矩阵 $\mathbf{A}$，是 $m$ 维空间的一组标准正交基。

这意味着，该空间中的任何一个 $m$ 维向量都可以由这组基线性表示。我们的矩阵 $\mathbf{B}$ 是一个 $m\times q$ 的矩阵，它的每一个列向量 ${\mathbf{\beta }}_k$ ($k=1,\dots ,q$) 都是一个 $m$ 维向量。因此，${\mathbf{\beta }}_k$ 可以表示为：

$${\mathbf{\beta }}_k=\sum _{j=1}^m{c}_{jk}{\mathbf{\alpha }}_j$$

其中，$c_{jk}$ 是向量 ${\mathbf{\beta }}_k$ 在基向量 ${\mathbf{\alpha }}_j$ 上的投影坐标。

将这 $q$ 个列向量的表达式合并，可以得到矩阵形式，即书中的 式(16.25)：

$$\mathbf{B}=\mathbf{AC}$$

这里，$\mathbf{A}$ 是 $m\times m$ 的基矩阵，$\mathbf{C}$ 是一个 $m\times q$ 的系数矩阵，其元素为 $c_{jk}$。

第二步：用新系数C重写目标函数

现在我们将 $\mathbf{B}=\mathbf{AC}$ 代入目标函数 $\text{tr}({\mathbf{B}}^T\mathbf{\Sigma B})$：

$$\begin{array}{rlrl}\text{tr}({\mathbf{B}}^T\mathbf{\Sigma B})& =\text{tr}\left((\mathbf{AC}{)}^T\mathbf{\Sigma }(\mathbf{AC})\right)& & \\ & =\text{tr}\left({\mathbf{C}}^T{\mathbf{A}}^T\mathbf{\Sigma AC}\right)& & \text{（利用转置性质 (XY)T=YTXT）}\end{array}$$

我们在 16.1.3 节已经知道，${\mathbf{A}}^T\mathbf{\Sigma A}=\mathbf{\Lambda }$，其中 $\mathbf{\Lambda }=\text{diag}({\lambda }_1,\dots ,{\lambda }_m)$ 是由 $\mathbf{\Sigma }$ 的特征值构成的对角矩阵。于是上式变为：

$$\text{tr}\left({\mathbf{C}}^T\mathbf{\Lambda C}\right)$$

为了求解这个迹，我们利用迹的循环性质 $\text{tr}(XYZ)=\text{tr}(ZXY)$:

$$\begin{array}{rlrl}\text{tr}\left({\mathbf{C}}^T\mathbf{\Lambda C}\right)& =\text{tr}\left(\mathbf{\Lambda C}{\mathbf{C}}^T\right)& & \text{（令 X=CT,Y=Λ,Z=C）}\end{array}$$

令矩阵 $\mathbf{E}=\mathbf{C}{\mathbf{C}}^T$，这是一个 $m\times m$ 的矩阵。其对角线元素 $E_{jj}$ 是 $\mathbf{C}$ 的第 $j$ 行（记为 ${\mathbf{c}}_j^T$）与自身点乘的结果：$E_{jj}={\mathbf{c}}_j^T{\mathbf{c}}_j={\sum }_{k=1}^q{c}_{jk}^2$。 由于 $\mathbf{\Lambda }$ 是对角矩阵，$\text{tr}(\mathbf{\Lambda E})$ 的计算非常简单：

$$\text{tr}(\mathbf{\Lambda E})=\sum _{j=1}^m{\lambda }_j{E}_{jj}=\sum _{j=1}^m{\lambda }_j\left(\sum _{k=1}^q{c}_{jk}^2\right)=\sum _{j=1}^m\sum _{k=1}^q{\lambda }_j{c}_{jk}^2$$

这就是书中的 式(16.26)，我们把目标函数成功地用系数 $c_{jk}$ 表示了出来。

第三步：用新系数C重写约束条件

我们的原始约束是 $\mathbf{B}$ 的列向量标准正交，即 ${\mathbf{B}}^T\mathbf{B}={\mathbf{I}}_q$。同样代入 $\mathbf{B}=\mathbf{AC}$：

$${\mathbf{B}}^T\mathbf{B}=(\mathbf{AC}{)}^T(\mathbf{AC})={\mathbf{C}}^T{\mathbf{A}}^T\mathbf{AC}={\mathbf{C}}^T{\mathbf{I}}_m\mathbf{C}={\mathbf{C}}^T\mathbf{C}={\mathbf{I}}_q$$

约束条件巧妙地转化为了对系数矩阵 $\mathbf{C}$ 的约束：${\mathbf{C}}^T\mathbf{C}={\mathbf{I}}_q$。==这表明，矩阵 $\mathbf{C}$ 的 $q$ 个列向量也是标准正交的。==

这个约束还隐含了另一个重要性质，即 式(16.28) 的由来：

1. 首先，由 ${\mathbf{C}}^T\mathbf{C}={\mathbf{I}}_q$，取迹可得 式(16.27):

   $$\text{tr}({\mathbf{C}}^T\mathbf{C})=\text{tr}({\mathbf{I}}_q)=q⟹\sum _{k=1}^q\sum _{j=1}^m{c}_{jk}^2=q$$

2. 其次，由于 $\mathbf{C}$ 的列是标准正交的，我们可以将这 $q$ 个 $m$ 维列向量看作是某个 $m\times m$ 正交矩阵 $\mathbf{D}$ 的前 $q$ 列。

3. 因为 $\mathbf{D}$ 是正交矩阵，所以它的行向量也是标准正交的，即每一行的模长为1。

4. $\mathbf{C}$ 的第 $j$ 行只是 $\mathbf{D}$ 的第 $j$ 行的前 $q$ 个元素。因此，$\mathbf{C}$ 的第 $j$ 行的模长平方必然小于等于其所在母体（$\mathbf{D}$ 的第 $j$ 行）的模长平方（即1）。

   $$\sum _{k=1}^q{c}_{jk}^2\le 1\text{for }j=1,\dots ,m$$

   这就是 式(16.28)。

第四步：求解最终的优化问题

现在，我们的问题被彻底转化为一个关于系数 $c_{jk}$ 的优化问题：

$$\underset{\{c_{jk}\}}{\max }\sum _{j=1}^m{\lambda }_j\left(\sum _{k=1}^q{c}_{jk}^2\right)$$

约束条件为：

1. ${\sum }_{j=1}^m\left({\sum }_{k=1}^q{c}_{jk}^2\right)=q$
2. ${\sum }_{k=1}^q{c}_{jk}^2\le 1$ (对每个 $j$)

这是一个经典的资源分配问题。我们将总量为 $q$ 的“能量”（$\sum \sum c_{jk}^2$）分配给 $m$ 个“项目”（由 $j$ 索引），每个项目的“回报率”是 ${\lambda }_j$。为了使总回报最大，我们自然应该将所有能量优先分配给回报率最高的项目。

由于特征值已经排序 ${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_m$，最优策略是：

• 将前 $q$ 个项目的能量槽加满：${\sum }_{k=1}^q{c}_{jk}^2=1$ for $j=1,\dots ,q$
• 不给后面的项目分配任何能量：${\sum }_{k=1}^q{c}_{jk}^2=0$ for $j=q+1,\dots ,m$

这个分配方案满足所有约束条件。这个条件对应 式(16.29)。

满足这个条件的最简洁的系数矩阵 $\mathbf{C}$ 是：

$$\mathbf{C}=\left(\begin{array}{c}{\mathbf{I}}_q\\ 0_{(m-q)\times q}\end{array}\right)$$

即一个 $m\times q$ 矩阵，其左上角是 $q\times q$ 的单位阵，其余部分是零。 此时，最优的 $\mathbf{B}$ 为：

$$\mathbf{B}=\mathbf{AC}=[{\alpha }_1,\dots ,{\alpha }_m]\left(\begin{array}{c}{\mathbf{I}}_q\\ 0\end{array}\right)=[{\alpha }_1,\dots ,{\alpha }_q]={\mathbf{A}}_q$$

定理16.2证毕。这证明了，要用 $q$ 个维度最大化保留原始方差，就必须选择前 $q$ 个主成分。

方差贡献率

在实际操作中，我们用以下指标来决定要保留的主成分个数 $k$：

• 定义16.2 第k主成分的方差贡献率 (Variance Contribution Rate):

  $${\eta }_k=\frac{{\lambda }_k}{{\sum }_{i=1}^m{\lambda }_i}$$

  它表示第 $k$ 个主成分保留了总方差的百分之多少。

• k个主成分的累计方差贡献率 (Cumulative Variance Contribution Rate):

  $$K_k=\sum _{i=1}^k{\eta }_i=\frac{{\sum }_{i=1}^k{\lambda }_i}{{\sum }_{i=1}^m{\lambda }_i}$$

  它表示前 $k$ 个主成分一共保留了总方差的百分之多少。通常我们会设定一个阈值（如80%, 90%），选择使 $K_k$ 首次超过该阈值的 $k$ 作为降维后的维度。

---

规范化变量的总体主成分

这一节处理一个非常实际的问题：当原始数据中不同变量的单位或量级相差悬殊时，直接做PCA是不合理的。

量纲带来的影响

PCA的核心是最大化方差。如果一个变量的数值很大（例如用“克”作单位的体重），其方差会远大于数值小的变量（例如用“米”作单位的身高）。这会导致方差大的变量在主成分中占据绝对主导地位，而方差小的变量几乎被忽略，这与变量本身的实际重要性无关，仅仅是单位选择的结果。

使用变量规范化消除量纲影响

为了让每个变量在分析中具有同等地位，我们先对其进行规范化（或称标准化），如 式(16.33) 所示：

$$x_i^{\ast }=\frac{x_i-E(x_i)}{\sqrt{\text{var}(x_i)}}=\frac{x_i-{\mu }_i}{\sqrt{{\sigma }_{ii}}}$$

经过规范化后，新的变量 $x_i^{\ast }$ 具有如下优良特性：

• 均值 $E(x_i^{\ast })=0$
• 方差 $\text{var}(x_i^{\ast })=1$

PCA作用于相关矩阵R

对规范化后的变量 $x^{\ast }$ 做PCA，等价于对它们的协方差矩阵进行特征值分解。我们来计算这个新的协方差矩阵：

$$\begin{array}{rl}\text{cov}(x_i^{\ast },x_j^{\ast })& =E[x_i^{\ast }{x}_j^{\ast }]-E[x_i^{\ast }]E[x_j^{\ast }]\\ & =E\left[\left(\frac{x_i-{\mu }_i}{\sqrt{{\sigma }_{ii}}}\right)\left(\frac{x_j-{\mu }_j}{\sqrt{{\sigma }_{jj}}}\right)\right]-0\cdot 0\\ & =\frac{E[(x_i-{\mu }_i)(x_j-{\mu }_j)]}{\sqrt{{\sigma }_{ii}}\sqrt{{\sigma }_{jj}}}\\ & =\frac{\text{cov}(x_i,x_j)}{\sqrt{\text{var}(x_i)}\sqrt{\text{var}(x_j)}}\end{array}$$

这个最终的表达式正是原始变量 $x_i$ 和 $x_j$ 的相关系数 ${\rho }_{ij}$ 的定义！

结论: 对规范化变量 $x^{\ast }$ 进行主成分分析，等价于对原始变量的相关矩阵 R 进行主成分分析。

规范化主成分的性质

所有之前基于协方差矩阵 $\mathbf{\Sigma }$ 的性质，现在都可以平行地应用于相关矩阵 $\mathbf{R}$。我们只需做如下替换：$\mathbf{\Sigma }\to \mathbf{R}$, ${\lambda }_k\to {\lambda }_k^{\ast }$, ${\alpha }_k\to {\mathbf{e}}_k^{\ast }$, ${\sigma }_{ii}\to \text{var}(x_i^{\ast })=1$。

1. 性质(1): 规范化主成分的协方差矩阵 变换后的新变量 $y^{\ast }$ 的协方差矩阵是对角矩阵，对角元素是相关矩阵 $\mathbf{R}$ 的特征值：

   $${\mathbf{\Lambda }}^{\ast }=\text{diag}({\lambda }_1^{\ast },{\lambda }_2^{\ast },\dots ,{\lambda }_m^{\ast })$$

2. 性质(2): 总方差 总方差不变，且等于矩阵的维度 $m$：

   $$\sum _{k=1}^m{\lambda }_k^{\ast }=\text{tr}(\mathbf{R})=\sum _{i=1}^m{\rho }_{ii}=\sum _{i=1}^{m}1=m$$

3. 性质(3): 因子负荷量 (Factor Loading) 第 $k$ 个主成分 $y_k^{\ast }$ 与第 $i$ 个规范化原始变量 $x_i^{\ast }$ 的相关系数为：

   $$\rho (y_k^{\ast },x_i^{\ast })=\sqrt{{\lambda }_k^{\ast }}{e}_{ik}^{\ast }$$

   （推导：$\rho =\frac{\text{cov}(y_k^{\ast },x_i^{\ast })}{\sqrt{\text{var}(y_k^{\ast })\text{var}(x_i^{\ast })}}=\frac{{\lambda }_k^{\ast }{e}_{ik}^{\ast }}{\sqrt{{\lambda }_k^{\ast }\cdot 1}}=\sqrt{{\lambda }_k^{\ast }}{e}_{ik}^{\ast }$。其中 $e_{ik}^{\ast }$ 是 $\mathbf{R}$ 的第 $k$ 个特征向量 ${\mathbf{e}}_k^{\ast }$ 的第 $i$ 个分量。）

4. 性质(4): 单个主成分的因子负荷量平方和 第 $k$ 个主成分 $y_k^{\ast }$ 与所有原始变量的相关系数的平方和等于其方差（即对应的特征值）：

   $$\sum _{i=1}^m{\rho }^2(y_k^{\ast },x_i^{\ast })=\sum _{i=1}^m(\sqrt{{\lambda }_k^{\ast }}{e}_{ik}^{\ast }{)}^2={\lambda }_k^{\ast }\sum _{i=1}^m(e_{ik}^{\ast }{)}^2={\lambda }_k^{\ast }\cdot 1={\lambda }_k^{\ast }$$

   （因为 ${\mathbf{e}}_k^{\ast }$ 是单位向量，其分量平方和为1。）

5. 性质(5): 单个原始变量的因子负荷量平方和 第 $i$ 个原始变量 $x_i^{\ast }$ 与所有主成分的相关系数的平方和等于1：

   $$\sum _{k=1}^m{\rho }^2(y_k^{\ast },x_i^{\ast })=1$$

   这表明，所有的主成分合在一起，可以完全解释每一个（规范化后的）原始变量的方差（方差为1）。