主成分分析PCA-样本主成分分析

**从“总体”到“样本”

• 在总体PCA中：我们假设拥有上帝视角，知道随机变量 $\mathbf{x}$ 的真实均值 $\mu$ 和真实协方差矩阵 $\mathbf{\Sigma }$。我们所有的推导都基于这两个已知的“真值”。
• 在样本PCA中：我们回归现实。我们没有上帝视角，只有一组从总体中抽取的、有限的观测数据。我们能做的，就是利用这组数据估计出总体的均值和协方差。然后，将总体PCA中所有的理论和方法，应用到这些估计值上。

简而言之：用样本均值 $\bar{\mathbf{x}}$ 替代总体均值 $\mu$，用样本协方差矩阵 $\mathbf{S}$ 替代总体协方差矩阵 $\mathbf{\Sigma }$。

---

1. 数据与统计量的定义

1.1 样本数据矩阵 X

在实际问题中，我们的数据通常以一个矩阵的形式存在。

• 定义：假设我们对 $m$ 个变量（特征）进行了 $n$ 次独立观测。所有数据可以构成一个 $m\times n$ 的样本矩阵 $\mathbf{X}$。

  $$\mathbf{X}=[{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_n]=\left[\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1n}\\ x_{21}& x_{22}& \cdots & x_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ x_{m1}& x_{m2}& \cdots & x_{mn}\end{array}\right]$$

• 解读：

  • 每一列 ${\mathbf{x}}_j=(x_{1j},x_{2j},\dots ,x_{mj}{)}^T$ 代表第 $j$ 次观测得到的样本，包含所有 $m$ 个变量的值。
  • 每一行代表第 $i$ 个变量在所有 $n$ 次观测中的取值。
  • $x_{ij}$ 表示第 $j$ 次观测时，第 $i$ 个变量的值。

1.2 样本均值向量 $\bar{\mathbf{x}}$

这是对总体均值 $\mu$ 的估计。

• 定义 (式16.40)：

  $$\bar{\mathbf{x}}=\frac{1}{n}\sum _{j=1}^n{\mathbf{x}}_j$$

• 这是一个 $m\times 1$ 的列向量。它的第 $i$ 个元素 ${\bar{x}}_i=\frac{1}{n}{\sum }_{j=1}^n{x}_{ij}$，就是第 $i$ 个变量在所有 $n$ 次观测中的平均值。它就是对数据矩阵 $\mathbf{X}$ 的所有列向量求平均。

1.3 样本协方差矩阵 S

这是对总体协方差矩阵 $\mathbf{\Sigma }$ 的估计，也是样本PCA的核心计算对象。

• 定义 (式16.41)：$\mathbf{S}=[s_{ij}{]}_{m\times m}$ 是一个 $m\times m$ 的对称矩阵，其元素 $s_{ij}$ 计算如下：

  $$s_{ij}=\frac{1}{n-1}\sum _{k=1}^n(x_{ik}-{\bar{x}}_i)(x_{jk}-{\bar{x}}_j)$$

• 对角线元素 $s_{ii}$: 这是第 $i$ 个变量的样本方差，衡量该变量自身的离散程度。

• 非对角线元素 $s_{ij}$: 这是第 $i$ 和第 $j$ 个变量的样本协方差，衡量这两个变量的线性相关程度。

• 为什么是 $n-1$？: 这里的除数是 $n-1$ 而不是 $n$，这被称为“贝塞尔校正”。使用 $n-1$ 计算出的样本方差/协方差是对总体方差/协方差的无偏估计。通俗讲，这意味着如果我们从同一个总体中反复抽取多组样本并计算 $s_{ij}$，这些 $s_{ij}$ 的平均值会更接近真实的 ${\sigma }_{ij}$。而如果用 $n$ 作分母，估计值会系统性地偏低。

• 矩阵形式（更便于计算和理解）:

  1. 首先，对数据进行中心化：将每个观测向量 ${\mathbf{x}}_j$ 减去样本均值向量 $\bar{\mathbf{x}}$，得到中心化后的数据矩阵 ${\mathbf{X}}_c$。

  2. 然后，样本协方差矩阵可以非常简洁地表示为：

     $$\mathbf{S}=\frac{1}{n-1}{\mathbf{X}}_c{\mathbf{X}}_c^T$$

---

【数值示例】

我们用一个具体例子再来理解一下这些概念。假设我们有3个学生（$n=3$）的数学和物理成绩（$m=2$）：

学生	数学 ($x_1$)	物理 ($x_2$)
A	80	85
B	90	95
C	100	105

1. 数据矩阵 X:

   $$\mathbf{X}=\left[\begin{array}{ccc}80& 90& 100\\ 85& 95& 105\end{array}\right]$$

2. 样本均值向量 $\bar{\mathbf{x}}$:

   $${\bar{x}}_1=\frac{80+90+100}{3}=90(\text{数学平均分})$$ $${\bar{x}}_2=\frac{85+95+105}{3}=95(\text{物理平均分})$$ $$\bar{\mathbf{x}}=\left(\begin{array}{c}90\\ 95\end{array}\right)$$

3. 样本协方差矩阵 S: 首先，计算中心化矩阵 ${\mathbf{X}}_c$:

   $${\mathbf{X}}_c=\left[\begin{array}{ccc}80-90& 90-90& 100-90\\ 85-95& 95-95& 105-95\end{array}\right]=\left[\begin{array}{ccc}-10& 0& 10\\ -10& 0& 10\end{array}\right]$$

   现在计算 $\mathbf{S}=\frac{1}{3-1}{\mathbf{X}}_c{\mathbf{X}}_c^T$:

   $$\begin{array}{rl}\mathbf{S}& =\frac{1}{2}\left[\begin{array}{ccc}-10& 0& 10\\ -10& 0& 10\end{array}\right]\left[\begin{array}{cc}-10& -10\\ 0& 0\\ 10& 10\end{array}\right]\\ & =\frac{1}{2}\left[\begin{array}{cc}(-10)(-10)+0+10(10)& (-10)(-10)+0+10(10)\\ (-10)(-10)+0+10(10)& (-10)(-10)+0+10(10)\end{array}\right]\\ & =\frac{1}{2}\left[\begin{array}{cc}200& 200\\ 200& 200\end{array}\right]=\left[\begin{array}{cc}100& 100\\ 100& 100\end{array}\right]\end{array}$$
   • $s_{11}=100$ 是数学成绩的样本方差。
   • $s_{22}=100$ 是物理成绩的样本方差。
   • $s_{12}=100$ 是两者之间的样本协方差。这个例子中，两者完全正相关。

---

2. 样本主成分的定义

有了样本统计量 $\bar{\mathbf{x}}$ 和 $\mathbf{S}$，那么其实样本主成分的定义就是总体主成分定义的直接“复制-粘贴-替换”。

定义 16.4 (样本主成分)

给定样本矩阵 $\mathbf{X}$。样本第一主成分是 ${\mathbf{y}}_1={\mathbf{a}}_1^T\mathbf{x}$，其中 ${\mathbf{a}}_1$ 是在 ${\mathbf{a}}_1^T{\mathbf{a}}_1=1$ 条件下，使得 ${\mathbf{a}}_1^T{\mathbf{x}}_j$ ($j=1,\dots ,n$) 的样本方差 ${\mathbf{a}}_1^T\mathbf{S}{\mathbf{a}}_1$ 最大的线性变换。

… 以此类推，第 $i$ 个主成分是在 ${\mathbf{a}}_i^T{\mathbf{a}}_i=1$ 和 ${\mathbf{a}}_i^T\mathbf{S}{\mathbf{a}}_j=0$ ($j<i$) 条件下，使得样本方差 ${\mathbf{a}}_i^T\mathbf{S}{\mathbf{a}}_i$ 最大的线性变换。

• 这个定义构建的优化问题，与我们在总体PCA中解决的问题在数学形式上完全相同，只是把 $\mathbf{\Sigma }$ 换成了 $\mathbf{S}$。
  • 最大化目标: $\max {\mathbf{a}}^T\mathbf{Sa}$
  • 约束: ${\mathbf{a}}^T\mathbf{a}=1$
• 求解方法: 因此，求解方法也完全一样。我们不需要重新证明。
  • 样本主成分的求解，就是对样本协方差矩阵 $\mathbf{S}$ 进行特征值分解。
  • 第 $k$ 个样本主成分的方向向量 ${\mathbf{a}}_k$，就是 $\mathbf{S}$ 的第 $k$ 大特征值 ${\lambda }_k$ 所对应的单位特征向量。
  • 第 $k$ 个样本主成分的样本方差，就是特征值 ${\lambda }_k$。

---

3. 规范化与样本相关矩阵 R

与总体PCA一样，当变量单位或量级不同时，我们需要先对样本数据进行规范化。

• 规范化公式 (式16.48): 对每个观测值 $x_{ij}$，进行如下变换：

  $$x_{ij}^{\ast }=\frac{x_{ij}-{\bar{x}}_i}{\sqrt{s_{ii}}}$$

  其中 ${\bar{x}}_i$ 是第 $i$ 个变量的样本均值， $s_{ii}$ 是其样本方差。

• 作用于样本相关矩阵 R:

  • 定义 (式16.42)：样本相关矩阵 $\mathbf{R}=[r_{ij}]$ 的元素为：

    $$r_{ij}=\frac{s_{ij}}{\sqrt{s_{ii}{s}_{jj}}}$$

  • 对规范化后的样本数据做PCA，等价于对样本相关矩阵 $\mathbf{R}$ 进行特征值分解。

• 关于式(16.49)的说明: 书中提到，对于规范化后的数据矩阵（书中为方便记作 $\mathbf{X}$），样本协方差矩阵 $\mathbf{S}$ 就是样本相关矩阵 $\mathbf{R}$，并给出了公式 $\mathbf{R}=\frac{1}{n}\mathbf{X}{\mathbf{X}}^T$。 这里需要注意，这与之前定义的 $\mathbf{S}=\frac{1}{n-1}{\mathbf{X}}_c{\mathbf{X}}_c^T$ 在分母上有差异。

  • 使用 $n-1$ 是为了获得无偏估计，在统计推断中更常用。
  • 使用 $n$ 得到的是最大似然估计（在高斯假设下），在某些机器学习文献或算法实现中为了计算方便也可能出现。 在实际应用中，当样本量 $n$ 很大时，两者差异可以忽略。但理解其来源非常重要。在后续算法中，我们通常遵循先中心化，再计算 (1/(n-1)) * X_c * X_cᵀ 的标准流程。

至此，我们已经建立了样本PCA的完整逻辑。其算法步骤非常清晰：

1. 数据准备: 获取 $m\times n$ 的数据矩阵 $\mathbf{X}$。
2. （可选但强烈推荐）规范化: 如果各变量量纲不同，对 $\mathbf{X}$ 的每一行进行规范化处理。
3. 中心化: 计算样本均值向量 $\bar{\mathbf{x}}$，并将 $\mathbf{X}$ 的每一列都减去 $\bar{\mathbf{x}}$，得到中心化矩阵 ${\mathbf{X}}_c$。
4. 计算协方差/相关矩阵: 计算样本协方差矩阵 $\mathbf{S}=\frac{1}{n-1}{\mathbf{X}}_c{\mathbf{X}}_c^T$。（如果步骤2做了规范化，那么这一步计算出的就是样本相关矩阵 $\mathbf{R}$）。
5. 特征值分解: 对矩阵 $\mathbf{S}$ (或 $\mathbf{R}$) 进行特征值分解，得到特征值 ${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_m$ 和对应的单位特征向量 ${\mathbf{a}}_1,{\mathbf{a}}_2,\dots ,{\mathbf{a}}_m$。
6. 获得主成分: 这些特征向量 ${\mathbf{a}}_k$ 就是我们寻找的主成分方向。

基于相关矩阵特征值分解的PCA

这个算法是样本主成分分析最直接、最经典的方法。其步骤如下：

输入：$m\times n$ 的样本矩阵 $\mathbf{X}$，需要降维到的维度 $k$（或一个累计方差贡献率阈值）。 输出：$k$ 个主成分的方向向量，以及每个样本点在这 $k$ 个主成分上的新坐标。

---

【步骤 1】对观测数据进行规范化处理

• 为了消除不同变量（特征）由于量纲和数值范围差异带来的影响，确保每个变量在分析中地位平等，我们对原始数据矩阵 $\mathbf{X}$ 的每一个元素 $x_{ij}$（第 $i$ 个变量，第 $j$ 个样本）应用 式(16.48)：

  $$x_{ij}\leftarrow \frac{x_{ij}-{\bar{x}}_i}{\sqrt{s_{ii}}}$$

  其中，${\bar{x}}_i=\frac{1}{n}{\sum }_{j=1}^n{x}_{ij}$ 是第 $i$ 个变量的样本均值，而 $s_{ii}=\frac{1}{n-1}{\sum }_{j=1}^n(x_{ij}-{\bar{x}}_i{)}^2$ 是其样本方差。

• 经过上述操作得到规范化数据矩阵，书中为了方便，仍记作 $\mathbf{X}$。这个新矩阵的每一行（每个变量）的均值为0，方差为1。

【步骤 2】计算样本相关矩阵 R

• 而为了得到描述规范化后各变量之间线性关系的核心矩阵，我们根据 式(16.49)，计算 $m\times m$ 的样本相关矩阵 $\mathbf{R}$。

  $$\mathbf{R}=\frac{1}{n-1}\mathbf{X}{\mathbf{X}}^T$$

  （这里的 $\mathbf{X}$ 是上一步规范化后的矩阵）。

• 注意：由于上一步已经对数据进行了规范化处理（每一行的均值为0），所以这一步相当于直接计算规范化数据的协方差矩阵，其结果就是相关矩阵。

【步骤 3】求 R 的特征值和特征向量

• 然后，我们通过一个标准的线性代数计算找出主成分的方向和它们所能解释的方差大小。
  1. 求解特征方程：$|\mathbf{R}-\lambda \mathbf{I}|=0$，得到 $m$ 个特征值。
  2. 排序特征值：将特征值从大到小排列：${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_m\ge 0$。
  3. 确定主成分个数 k:
     • 方法A (指定个数)：如果问题直接给定了 $k$ 值。
     • 方法B (阈值法)：计算累计方差贡献率 ${\sum }_{i=1}^k{\eta }_i=\frac{{\sum }_{i=1}^k{\lambda }_i}{{\sum }_{i=1}^m{\lambda }_i}$，找到满足阈值（如75%）的最小 $k$。
  4. 求特征向量: 求解方程 $(\mathbf{R}-{\lambda }_i\mathbf{I}){\mathbf{a}}_i=0$，求出与前 $k$ 个特征值 ${\lambda }_1,\dots ,{\lambda }_k$ 对应的单位特征向量 ${\mathbf{a}}_1,\dots ,{\mathbf{a}}_k$。

【步骤 4 & 6】计算 k 个样本主成分和每个样本的主成分值

• 目的：定义新的坐标轴（主成分），并计算出每个原始样本点在新坐标系下的坐标。
• 操作：

  1. 定义主成分 (式16.50)：第 $i$ 个主成分 $y_i$ 是一个由原始变量构成的线性组合，其系数由特征向量 ${\mathbf{a}}_i$ 给出：

     $$y_i={\mathbf{a}}_i^T\mathbf{x}=a_{1i}{x}_1+a_{2i}{x}_2+\cdots +a_{mi}{x}_m$$

  2. 计算每个样本的主成分值: 对于第 $j$ 个样本（中心化/规范化后） ${\mathbf{x}}_j$，其在第 $i$ 个主成分上的坐标（或称“得分”）为 $y_{ij}$：

     $$y_{ij}={\mathbf{a}}_i^T{\mathbf{x}}_j=\sum _{l=1}^m{a}_{li}{x}_{lj}$$

【步骤 5】计算主成分的性质

• 目的：解释主成分的实际意义，并评估降维效果。
• 操作:

  1. 因子负荷量 (Factor Loadings)：计算第 $i$ 个主成分 $y_i$ 与第 $j$ 个原始变量 $x_j$ 的相关系数 $\rho (y_i,x_j)$。由于数据已规范化，公式简化为：

     $$\rho (y_i,x_j)=\sqrt{{\lambda }_i}{a}_{ji}$$

  2. 对变量 $x_j$ 的贡献率: 计算前 $k$ 个主成分对原始变量 $x_j$ 的方差的解释比例，即相关系数的平方和：

     $${\nu }_j=\sum _{i=1}^k{\rho }^2(y_i,x_j)$$

---

学生考试成绩分析

现在，我们用这个算法流程来一步步“复盘”书中的例子。

背景：分析 $n$ 个学生四门课程（语文$x_1$, 外语$x_2$, 数学$x_3$, 物理$x_4$）的成绩。

步骤 1 & 2 已完成

书上直接给出了对原始成绩数据进行规范化处理后，计算得到的样本相关矩阵 R (表 16.1)。

$$\mathbf{R}=\left[\begin{array}{cccc}1.00& 0.44& 0.29& 0.33\\ 0.44& 1.00& 0.35& 0.32\\ 0.29& 0.35& 1.00& 0.60\\ 0.33& 0.32& 0.60& 1.00\end{array}\right]$$

• 对角线全为1，这是相关矩阵的必然特征（变量与自身的相关性为1）。
• 非对角线元素 $r_{ij}$ 表示变量 $i$ 和 $j$ 的相关性。例如，$r_{34}=0.60$ 表示数学和物理成绩有较强的正相关，这符合直觉。$r_{13}=0.29$ 表示语文和数学相关性较弱。

步骤 3：求 R 的特征值和特征向量

• 特征值: ${\lambda }_1=2.17$, ${\lambda }_2=0.87$, ${\lambda }_3=0.57$, ${\lambda }_4=0.39$
• 总方差: $\sum {\lambda }_i=2.17+0.87+0.57+0.39=4.00$。这正好等于矩阵的维度 $m=4$，验证了规范化PCA的性质。
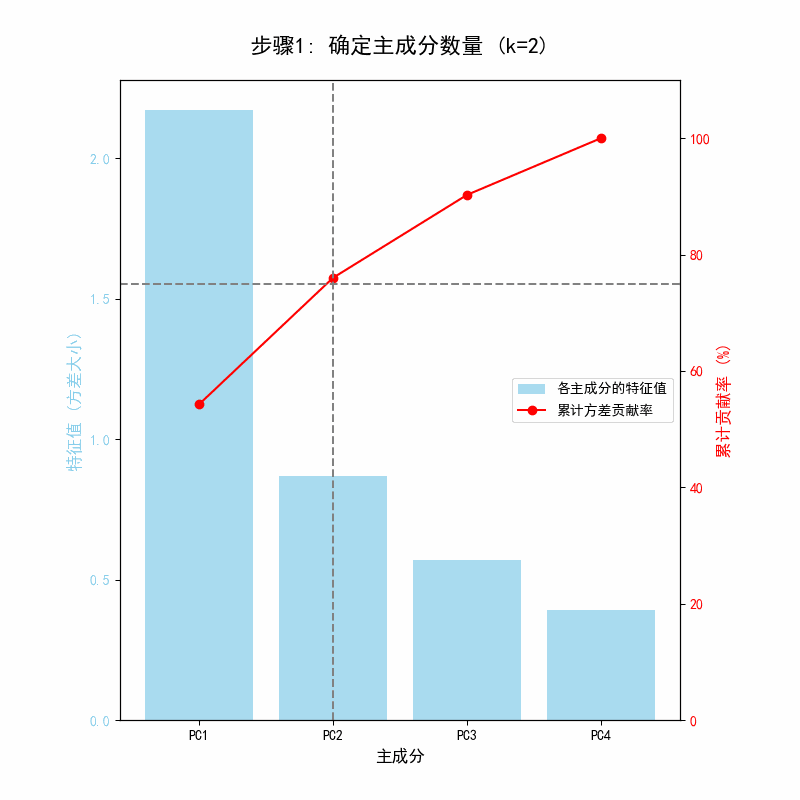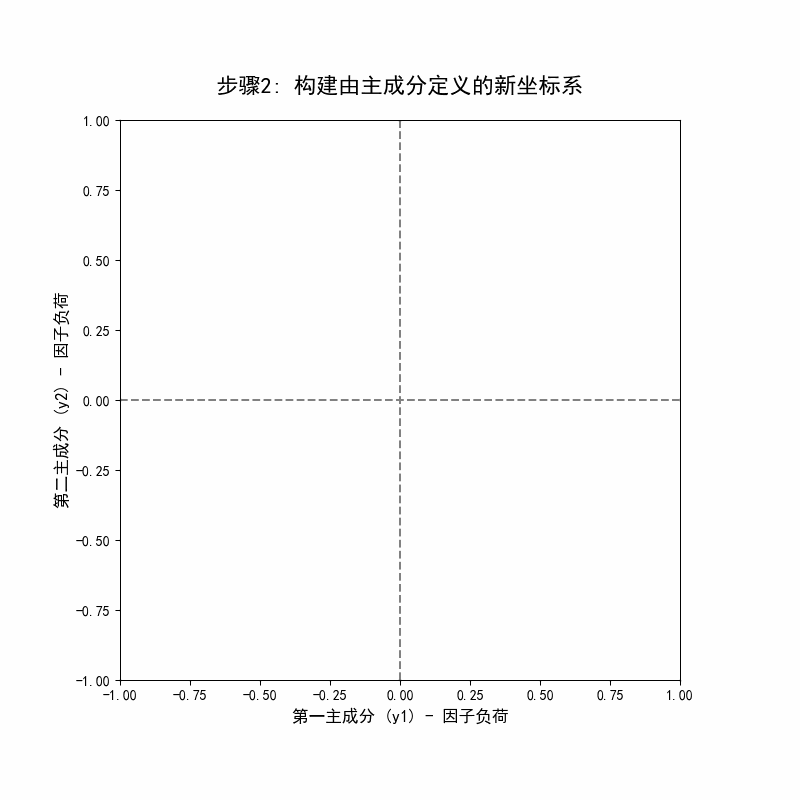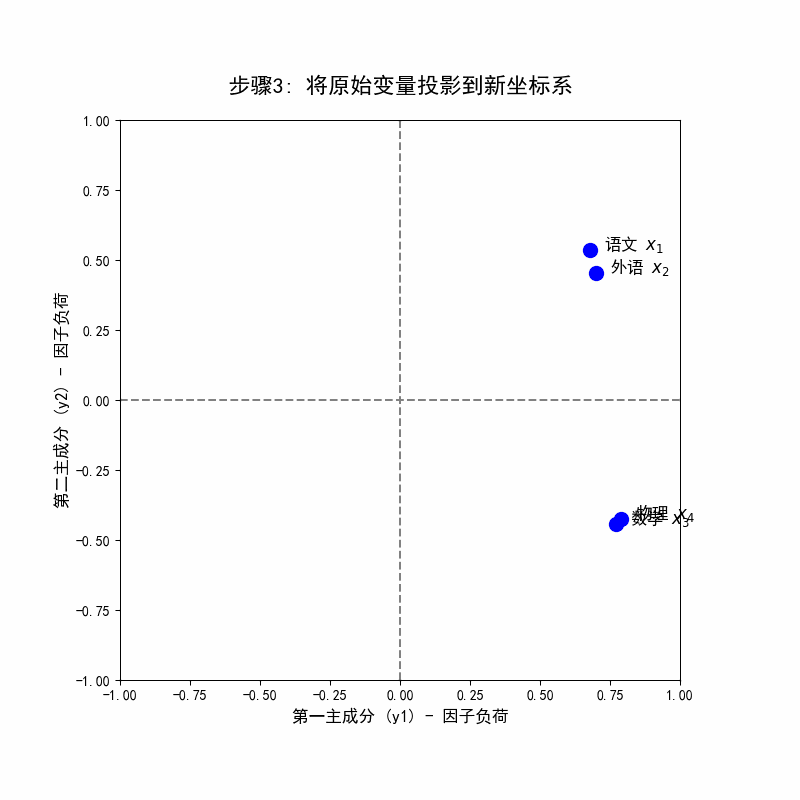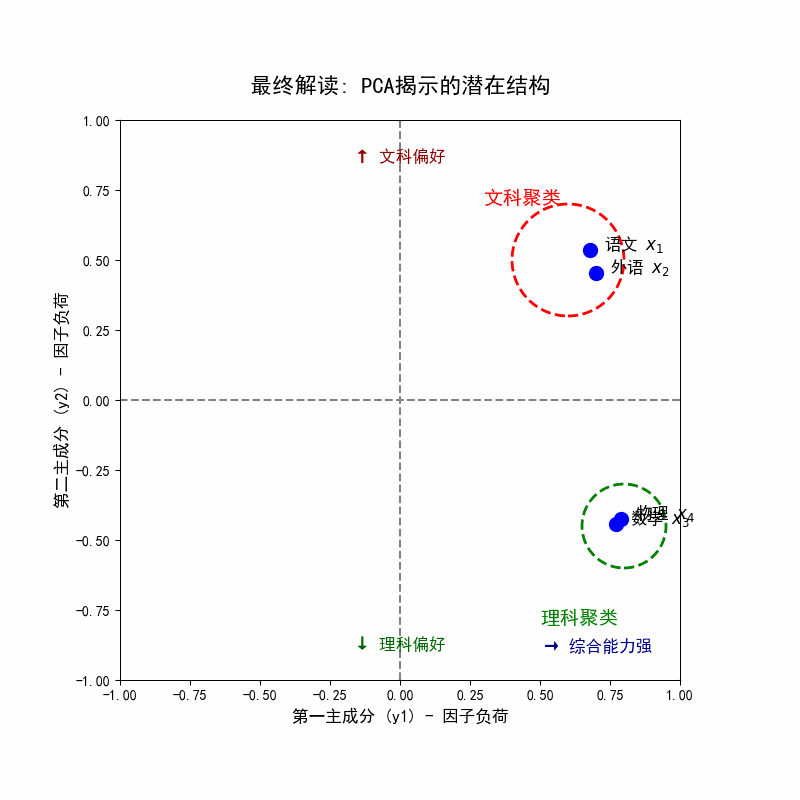
• 确定 k: 题目要求累计方差贡献率达到75%。
  • $k=1$: 贡献率 = ${\lambda }_1/4=2.17/4=0.543$ (54.3%)，不够。
  • $k=2$: 累计贡献率 = $({\lambda }_1+{\lambda }_2)/4=(2.17+0.87)/4=3.04/4=0.76$ (76%)。
  • 结论: 76% > 75%，所以我们选择 $k=2$，即保留前两个主成分。
• 特征向量 (表 16.2): 前两个特征值对应的单位特征向量：
  • ${\mathbf{a}}_1=(0.460,0.476,0.523,0.537{)}^T$ (对应 ${\lambda }_1=2.17$)
  • ${\mathbf{a}}_2=(0.574,0.486,-0.476,-0.456{)}^T$ (对应 ${\lambda }_2=0.87$)

步骤 4：定义前两个主成分

根据 式(16.50)，我们可以写出第一、第二主成分的表达式：

• 第一主成分 $y_1$:

  $$y_1=0.460x_1+0.476x_2+0.523x_3+0.537x_4$$

• 第二主成分 $y_2$:

  $$y_2=0.574x_1+0.486x_2-0.476x_3-0.456x_4$$

步骤 5：解读主成分的性质 (表 16.3)

这是PCA中最需要洞察力的部分，它赋予了数学计算结果实际的意义。

1. 计算因子负荷量 $\rho (y_i,x_j)=\sqrt{{\lambda }_i}{a}_{ji}$:

   • 对于 $y_1$: ($\sqrt{{\lambda }_1}=\sqrt{2.17}\approx 1.473$)
     • $\rho (y_1,x_1)=1.473\times 0.460=0.678$
     • $\rho (y_1,x_2)=1.473\times 0.476=0.701$
     • $\rho (y_1,x_3)=1.473\times 0.523=0.770$
     • $\rho (y_1,x_4)=1.473\times 0.537=0.791$
   • 对于 $y_2$: ($\sqrt{{\lambda }_2}=\sqrt{0.87}\approx 0.933$)
     • $\rho (y_2,x_1)=0.933\times 0.574=0.536$
     • $\rho (y_2,x_2)=0.933\times 0.486=0.453$
     • $\rho (y_2,x_3)=0.933\times (-0.476)=-0.444$
     • $\rho (y_2,x_4)=0.933\times (-0.456)=-0.425$

2. 解读因子负荷量:

   • 解读 $y_1$: 观察 $\rho (y_1,x_j)$ 这一行，所有四个值都是较大的正数。这意味着，要提高 $y_1$ 的得分，需要所有四门课的成绩都提高。因此，$y_1$ 可以被解释为“学生的综合/整体成绩”或“学习能力因子”。书中称之为“整体成绩”。
   • 解读 $y_2$: 观察 $\rho (y_2,x_j)$ 这一行，我们看到正负号的分化。语文($x_1$)和外语($x_2$)的负荷为正，而数学($x_3$)和物理($x_4$)的负荷为负。这意味着，如果一个学生语文、外语成绩高，而数学、物理成绩低，他的 $y_2$ 得分会很高。反之，如果他理科好文科差，$y_2$ 得分会很低。因此，$y_2$ 反映了学生的偏科情况，可以解释为“文科 vs 理科”的偏好因子。书中称之为“理科成绩”。（更准确的叫法应该是“文科-理科”差异因子，因为正值代表文科优势）。

3. 计算对原始变量的贡献率 ${\nu }_j$:

   • ${\nu }_1(语文)={\rho }^2(y_1,x_1)+{\rho }^2(y_2,x_1)=0.678^2+0.536^2\approx 0.460+0.287=0.747$
   • 这意味着，前两个主成分 $y_1,y_2$ 共同解释了原始“语文”成绩方差的 74.7%。其他三门课的贡献率同理计算。

可视化解读

• 坐标系: 这张图将四个原始变量（语文、外语、数学、物理）作为点，画在由前两个主成分 $y_1,y_2$ 构成的二维平面上。
• 点的坐标: 每个变量点 $x_j$ 的坐标是它的因子负荷量 $(\rho (y_1,x_j),\rho (y_2,x_j))$。
  • 数学 $x_3$ 的坐标是 $(0.770,-0.444)$。
  • 语文 $x_1$ 的坐标是 $(0.678,0.536)$。
• 聚类现象:
  • 语文($x_1$)和外语($x_2$)在图上彼此靠近，它们都在 $y_2$ 轴的正半轴，可以被归为“文科”。
  • 数学($x_3$)和物理($x_4$)在图上彼此靠近，它们都在 $y_2$ 轴的负半轴，可以被归为“理科”。
  • 所有四个变量在 $y_1$ 轴上都有较大的正值，再次印证了 $y_1$ 是“综合成绩”的解释。
• 这张图直观地展示了主成分分析发现的潜在结构：学生的成绩表现，可以很好地被“综合能力”和“文理偏科”这两个新的、不相关的维度来描述。这就是PCA强大的降维与特征提取能力。

数据矩阵的奇异值分解（SVD）算法

1. 为什么要用SVD？

在上一节，我们确立了PCA的核心算法：

1. 中心化数据得到 ${\mathbf{X}}_c$。
2. 计算样本协方差矩阵 $\mathbf{S}=\frac{1}{n-1}{\mathbf{X}}_c{\mathbf{X}}_c^T$。
3. 对 $\mathbf{S}$ 进行特征值分解。

这个方法在理论上完美，但在实践中可能遇到两个问题：

• 计算成本高：如果我们的特征维度 $m$ 非常大（例如，处理图像数据时，$m$ 可能是几十万），那么协方差矩阵 $\mathbf{S}$ 将是一个 $m\times m$ 的巨大矩阵。仅仅是计算并存储它，就可能耗费大量的计算资源和内存。
• 数值不稳定性：计算 ${\mathbf{X}}_c{\mathbf{X}}_c^T$ 这个步骤，涉及到矩阵与其自身的乘积。这个过程可能会放大矩阵中的计算误差，导致数值上的不精确，尤其是在矩阵条件数比较大的情况下。

SVD算法提供了一条更优雅的路径，它直接作用于（经过变换的）数据矩阵，避免了上述问题。

---

2. SVD与协方差矩阵特征值分解的等价性

这是理解本节内容的关键所在。我们要证明：对数据矩阵做SVD，其结果与对协方差矩阵做特征值分解是等价的，并且可以直接得到主成分。

让我们严格地推导这个关系。

1. 准备工作：

   • 我们从中心化后的数据矩阵 $\mathbf{X}$ 开始（书中算法16.1的输入假定数据已中心化）。$\mathbf{X}$ 是一个 $m\times n$ 的矩阵。

   • 我们定义一个新的 $n\times m$ 矩阵 ${\mathbf{X}}^{\prime }$，如 式(16.51) 所示：

     $${\mathbf{X}}^{\prime }=\frac{1}{\sqrt{n-1}}{\mathbf{X}}^T$$

     为什么要这样定义？ 这是一个巧妙的构造，它的目的是让后续的计算能直接产生我们想要的样本协方差矩阵。

2. 建立联系：我们来计算 ${\mathbf{X}}^{\prime T}{\mathbf{X}}^{\prime }$：

   $$\begin{array}{rlrl}{\mathbf{X}}^{\prime T}{\mathbf{X}}^{\prime }& ={\left(\frac{1}{\sqrt{n-1}}{\mathbf{X}}^T\right)}^T\left(\frac{1}{\sqrt{n-1}}{\mathbf{X}}^T\right)& & \\ & =\left(\frac{1}{\sqrt{n-1}}\mathbf{X}\right)\left(\frac{1}{\sqrt{n-1}}{\mathbf{X}}^T\right)& & \text{（利用转置性质 (cA)T=cAT 和 (AT)T=A）}\\ & =\frac{1}{n-1}\mathbf{X}{\mathbf{X}}^T& & \text{（合并常数项）}\end{array}$$

   我们发现，$\frac{1}{n-1}\mathbf{X}{\mathbf{X}}^T$ 正是我们定义的样本协方差矩阵 $\mathbf{S}$（在数据已中心化的情况下）！ 所以，我们得到了一个至关重要的恒等式，即书中的 式(16.53)：

   $$\mathbf{S}={\mathbf{X}}^{\prime T}{\mathbf{X}}^{\prime }$$

   这意味着，我们想要求解特征值分解的协方差矩阵 $\mathbf{S}$，可以被表示为我们构造的矩阵 ${\mathbf{X}}^{\prime }$ 与其转置的乘积。

3. 引入SVD：现在，我们对矩阵 ${\mathbf{X}}^{\prime }$ 进行奇异值分解（SVD）：

   $${\mathbf{X}}^{\prime }=\mathbf{U\Sigma }{\mathbf{V}}^T$$

   其中：

   • $\mathbf{U}$ 是 $n\times n$ 的正交矩阵（左奇异向量）。
   • $\mathbf{\Sigma }$ 是 $n\times m$ 的矩形对角矩阵（奇异值）。
   • $\mathbf{V}$ 是 $m\times m$ 的正交矩阵（右奇异向量）。

4. 连接SVD与特征值分解: 将SVD的表达式代入到我们之前推导的 $\mathbf{S}={\mathbf{X}}^{\prime T}{\mathbf{X}}^{\prime }$ 中：

   $$\begin{array}{rlrl}\mathbf{S}& =(\mathbf{U\Sigma }{\mathbf{V}}^T{)}^T(\mathbf{U\Sigma }{\mathbf{V}}^T)& & \\ & =(\mathbf{V}{\mathbf{\Sigma }}^T{\mathbf{U}}^T)(\mathbf{U\Sigma }{\mathbf{V}}^T)& & \text{（应用转置性质 (ABC)T=CTBTAT）}\\ & =\mathbf{V}{\mathbf{\Sigma }}^T({\mathbf{U}}^T\mathbf{U})\mathbf{\Sigma }{\mathbf{V}}^T& & \text{（矩阵乘法结合律）}\end{array}$$

   由于 $\mathbf{U}$ 是正交矩阵，所以 ${\mathbf{U}}^T\mathbf{U}=\mathbf{I}$ （单位矩阵）。上式简化为：

   $$\mathbf{S}=\mathbf{V}({\mathbf{\Sigma }}^T\mathbf{\Sigma }){\mathbf{V}}^T$$

   让我们仔细看一下 ${\mathbf{\Sigma }}^T\mathbf{\Sigma }$ 这一项。$\mathbf{\Sigma }$ 是 $n\times m$ 的对角矩阵，其对角线上的前 $r$ (矩阵的秩) 个元素是奇异值 ${\sigma }_1,{\sigma }_2,\dots ,{\sigma }_r$。那么 ${\mathbf{\Sigma }}^T\mathbf{\Sigma }$ 会是一个 $m\times m$ 的对角矩阵，其对角线元素为 ${\sigma }_1^2,{\sigma }_2^2,\dots ,{\sigma }_r^2,0,\dots ,0$。

   如果我们令 $\mathbf{\Lambda }={\mathbf{\Sigma }}^T\mathbf{\Sigma }$，那么这个对角矩阵 $\mathbf{\Lambda }$ 的对角元就是我们想要的特征值。 此时，等式变为：

   $$\mathbf{S}=\mathbf{V\Lambda }{\mathbf{V}}^T⟹\mathbf{SV}=\mathbf{V\Lambda }$$

   这个形式 $\mathbf{SV}=\mathbf{V\Lambda }$ 正是协方差矩阵S的特征值分解的矩阵形式！

5. 得出结论：

   • 主成分方向: 比较 $\mathbf{SV}=\mathbf{V\Lambda }$ 和特征值分解的标准形式 $\mathbf{SA}=\mathbf{A\Lambda }$，我们发现，协方差矩阵 $\mathbf{S}$ 的特征向量矩阵 $\mathbf{A}$，恰好就是我们对 ${\mathbf{X}}^{\prime }$ 做SVD得到的右奇异向量矩阵 V！
   • 主成分方差: 协方差矩阵 $\mathbf{S}$ 的特征值 ${\lambda }_i$，恰好是 ${\mathbf{X}}^{\prime }$ 的奇异值 ${\sigma }_i$ 的平方，即 ${\lambda }_i={\sigma }_i^2$。

至此，我们从理论上完美证明了，通过对变换后的数据矩阵 ${\mathbf{X}}^{\prime }$ 进行SVD，我们就能直接获得主成分分析所需的一切信息，而无需计算S。

---

算法 16.1 (主成分分析算法)

现在，我们来逐行解析这个基于SVD的具体算法。

输入：$m\times n$ 样本矩阵 $\mathbf{X}$，且其每一行元素的均值为零（即数据已中心化）。需要降维到的维度 $k$。 输出：$k\times n$ 的样本主成分矩阵 $\mathbf{Y}$（即降维后的数据）。

【步骤 1】构造新的 n x m 矩阵 X’

• 操作:

  $${\mathbf{X}}^{\prime }=\frac{1}{\sqrt{n-1}}{\mathbf{X}}^T$$

• 如我们刚才所证明的，这个构造是为了让 ${\mathbf{X}}^{\prime T}{\mathbf{X}}^{\prime }$ 正好等于样本协方差矩阵 $\mathbf{S}$，从而在SVD和特征值分解之间建立桥梁。

【步骤 2】对矩阵 X’ 进行截断奇异值分解

• 操作: 对 ${\mathbf{X}}^{\prime }$ 进行SVD，但我们只需要保留前 $k$ 个最大的奇异值和对应的奇异向量。

  $${\mathbf{X}}^{\prime }\approx {\mathbf{U}}_k{\mathbf{\Sigma }}_k{\mathbf{V}}_k^T$$

  其中：

  • ${\mathbf{U}}_k$ 是 $n\times k$ 矩阵，包含前 $k$ 个左奇异向量。
  • ${\mathbf{\Sigma }}_k$ 是 $k\times k$ 对角矩阵，包含前 $k$ 个奇异值。
  • ${\mathbf{V}}_k$ 是 $m\times k$ 矩阵，包含前 $k$ 个右奇异向量。

• 根据我们的理论推导，${\mathbf{V}}_k$ 的列向量就是我们梦寐以求的前 $k$ 个主成分的方向向量！

【步骤 3】求 k x n 样本主成分矩阵 Y

• 目的: 将原始的 $n$ 个样本点，投影到由前 $k$ 个主成分构成的新的坐标空间中，得到它们的新坐标。

• 操作:

  $$\mathbf{Y}={\mathbf{V}}_k^T\mathbf{X}$$

• 注:

  • ${\mathbf{V}}_k$ 是一个 $m\times k$ 的矩阵，它的每一列是一个主成分方向。所以 ${\mathbf{V}}_k^T$ 是一个 $k\times m$ 的矩阵，它的每一行是一个主成分方向。
  • $\mathbf{X}$ 是原始的 $m\times n$ 数据矩阵。
  • 矩阵乘法 $\mathbf{Y}={\mathbf{V}}_k^T\mathbf{X}$ 的结果是一个 $k\times n$ 的矩阵。
  • 让我们看 $\mathbf{Y}$ 的第 $j$ 列 ${\mathbf{y}}_j={\mathbf{V}}_k^T{\mathbf{x}}_j$。这正是将原始的第 $j$ 个样本点 ${\mathbf{x}}_j$ 投影到由 ${\mathbf{V}}_k$ 的列向量张成的 $k$ 维子空间中，得到的新坐标。
  • 因此，矩阵 $\mathbf{Y}$ 的每一列，就是降维后对应样本点的新表示。

---

两种方法的比较与总结

特性	方法一：协方差矩阵的特征值分解	方法二：数据矩阵的SVD
核心计算对象	样本协方差矩阵 $\mathbf{S}$ ($m\times m$)	（变换后的）数据矩阵 ${\mathbf{X}}^{\prime }$ ($n\times m$)
核心数学运算	特征值分解 (Eigen-decomposition)	奇异值分解 (SVD)
主成分方向	$\mathbf{S}$ 的特征向量	${\mathbf{X}}^{\prime }$ 的右奇异向量 $\mathbf{V}$
主成分方差	$\mathbf{S}$ 的特征值 ${\lambda }_i$	${\mathbf{X}}^{\prime }$ 的奇异值的平方 ${\sigma }_i^2$
适用场景	当特征数 $m$ 远小于样本数 $n$ 时，尚可接受。	通用，特别是当 $m$ 很大时，优势明显。
优点	理论直观，易于理解。	数值稳定性好，计算效率高（有成熟的高效SVD算法库），无需构建巨大的S矩阵。

SVD方法是执行主成分分析在现代计算中的标准和首选方法。它不仅在数学上等价，而且在计算实践中表现更优越。我们在主流机器学习库（如Scikit-learn）中调用PCA时，其底层实现很大概率就是基于SVD的。