初识SVM

支持向量机 (Support Vector Machines, SVM)

1. SVM 的由来

1.1 问题的背景：二分类问题

在机器学习中，我们经常遇到二分类问题。给定一组带有标签的训练数据 $\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),\dots ,({\mathbf{x}}_N,y_N)\}$，其中 ${\mathbf{x}}_i\in {\mathbb{R}}^d$ 是 $d$ 维特征向量，$y_i\in \{-1,+1\}$ 是对应的类别标签（通常用 $-1$ 和 $+1$ 代表两个不同的类别）。我们的目标是学习一个模型，能够对新的输入 $\mathbf{x}$ 预测其类别 $y$。

对于线性可分的数据集，这意味着存在一个超平面，可以将不同类别的样本完全分开。

1.2 为什么需要 SVM？（超越感知机和逻辑回归）

在 SVM 出现之前，已经有一些线性分类算法，比如：

• 感知机 (Perceptron)：能够找到一个将数据线性分开的超平面。然而，感知机算法找到的超平面不唯一。对于一个线性可分的数据集，可能存在无数个这样的超平面，而感知机只能保证找到其中一个，但无法保证找到“最好”的那个。它对噪声敏感，并且泛化能力可能不佳。

• 逻辑回归 (Logistic Regression)：虽然也是线性模型，但它学习的是概率模型 $P(Y=1|\mathbf{x})$，通过 Sigmoid 函数将线性输出映射到 [0,1] 区间。逻辑回归寻找的是使训练数据似然度最大的参数。它输出概率，但其目标函数与“间隔”的概念没有直接联系，因此也无法保证找到一个鲁棒的决策边界。

SVM 的核心思想：最大间隔 (Maximum Margin)

SVM 的出现正是为了解决上述问题。它的核心理念是：找到一个不仅能将不同类别样本分开，而且能使两类样本之间间隔最大的超平面。

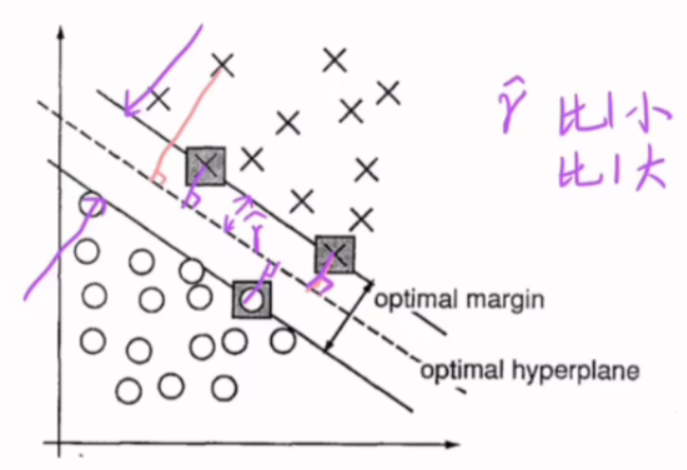
想象一下你在一个二维平面上，有两堆点（一类是圈圈，一类是叉叉）。

• 感知机可能找到任何一条直线，只要它能把圈圈和叉叉分开。
• SVM 则会找到一条特殊的直线，这条直线与两堆点中距离它最近的那些点之间，留有最宽的“空白地带”。这条“空白地带”的宽度，就是我们所说的“间隔”。

为什么最大间隔是“最好”的？ 直观上，这个“最宽的街道”决策边界具有更好的鲁棒性（对噪声或新样本的容错能力），因为它离两类样本都尽可能远。在实际应用中，这意味着更好的泛化能力，即模型在未见过的新数据上表现更好。

2. SVM 的学习问题（最大化几何间隔 (Hard Margin SVM)）

现在我们来形式化 SVM 的学习问题。我们首先考虑线性可分的情况，即存在一个超平面能将两类样本完美分开。这被称为硬间隔 SVM (Hard Margin SVM)。

2.1 线性分类器的表示

线性分类器由一个超平面定义。在 $d$ 维空间中，一个超平面可以用以下方程表示： ${\mathbf{w}}^T\mathbf{x}+b=0$ 其中：

• $\mathbf{w}=(w_1,w_2,\dots ,w_d{)}^T$ 是法向量，它决定了超平面的方向。
• $b$ 是偏置项（或截距），它决定了超平面在空间中的位置。

对于一个样本点 ${\mathbf{x}}_i$，我们通过计算其与超平面的“函数值”来判断其类别：

• 如果 ${\mathbf{w}}^T{\mathbf{x}}_i+b>0$，我们预测其为正类 ($y=+1$)。
• 如果 ${\mathbf{w}}^T{\mathbf{x}}_i+b<0$，我们预测其为负类 ($y=-1$)。

为了方便后续的数学推导，我们要求对于所有的训练样本 $({\mathbf{x}}_i,y_i)$：

• 如果 $y_i=+1$，那么 ${\mathbf{w}}^T{\mathbf{x}}_i+b>0$
• 如果 $y_i=-1$，那么 ${\mathbf{w}}^T{\mathbf{x}}_i+b<0$

这两个条件可以统一写成： $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)>0\text{对于所有 }i=1,\dots ,N$ 这表示所有样本都被正确分类。

2.2 函数间隔 (Functional Margin)

为了衡量一个点距离决策边界有多远以及分类的置信度，我们引入函数间隔 (Functional Margin)。 对于训练样本 $({\mathbf{x}}_i,y_i)$，其函数间隔定义为： ${\hat{\gamma }}_i=y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)$ 解释：

• 如果一个点被正确分类，则 $y_i$ 和 $({\mathbf{w}}^T{\mathbf{x}}_i+b)$ 的符号相同，所以 ${\hat{\gamma }}_i>0$。
• ${\hat{\gamma }}_i$ 的绝对值大小表示了点 ${\mathbf{x}}_i$ 距离超平面的远近（在不考虑 $\Vert \mathbf{w}\Vert$ 缩放的情况下）以及分类的置信度。${\hat{\gamma }}_i$ 越大，表示点离超平面越远，分类越正确、越自信。

整个训练数据集的函数间隔定义为所有样本函数间隔的最小值： $\hat{\gamma }={\min }_{i=1,\dots ,N}{\hat{\gamma }}_i={\min }_{i=1,\dots ,N}{y}_i({\mathbf{w}}^T{\mathbf{x}}_i+b)$ 函数间隔有一个问题：如果我们同时将 $\mathbf{w}$ 和 $b$ 乘以一个常数因子 $c>0$，即用 $(c\mathbf{w},cb)$ 来代替 $(\mathbf{w},b)$，那么超平面 ${\mathbf{w}}^T\mathbf{x}+b=0$ 不变，但函数间隔会变成 $c{\hat{\gamma }}_i$，从而函数间隔 $\hat{\gamma }$ 也会被缩放。这使得函数间隔不能直接衡量点到超平面的几何距离。

2.3 几何间隔 (Geometric Margin)

为了解决函数间隔的尺度不确定性问题，我们引入几何间隔 (Geometric Margin)。几何间隔是点到超平面的真正欧氏距离。 超平面 ${\mathbf{w}}^T\mathbf{x}+b=0$ 的法向量是 $\mathbf{w}$。从原点到超平面的距离是 $|b|/\Vert \mathbf{w}\Vert$。 对于任意点 ${\mathbf{x}}_i$ 到超平面的有向距离（即点在法向量方向上的投影），其欧氏距离（非负）为 $\frac{|{\mathbf{w}}^T{\mathbf{x}}_i+b|}{\Vert \mathbf{w}\Vert }$。 将类别标签 $y_i$ 考虑进去，几何间隔定义为： ${\gamma }_i=y_i\frac{{\mathbf{w}}^T{\mathbf{x}}_i+b}{\Vert \mathbf{w}\Vert }$ 解释：

• $\Vert \mathbf{w}\Vert =\sqrt{w_1^2+w_2^2+\cdots +w_d^2}$ 是向量 $\mathbf{w}$ 的L2范数，也称为欧氏范数。
• 几何间隔是真实距离，它不依赖于 $\mathbf{w}$ 和 $b$ 的具体数值，只依赖于它们之间的相对比例。如果你用 $(c\mathbf{w},cb)$ 代替 $(\mathbf{w},b)$，那么几何间隔为 $y_i\frac{c({\mathbf{w}}^T{\mathbf{x}}_i+b)}{\Vert c\mathbf{w}\Vert }=y_i\frac{c({\mathbf{w}}^T{\mathbf{x}}_i+b)}{|c|\Vert \mathbf{w}\Vert }=y_i\frac{{\mathbf{w}}^T{\mathbf{x}}_i+b}{\Vert \mathbf{w}\Vert }$ (假设 $c>0$)，保持不变。

整个数据集的几何间隔定义为所有样本几何间隔的最小值： $\gamma ={\min }_{i=1,\dots ,N}{\gamma }_i={\min }_{i=1,\dots ,N}{y}_i\frac{{\mathbf{w}}^T{\mathbf{x}}_i+b}{\Vert \mathbf{w}\Vert }$ SVM 的目标：找到一个超平面 $(\mathbf{w},b)$，使得所有样本都正确分类，并且几何间隔 $\gamma$ 最大化。

2.4 SVM 的优化问题 (初始形式)

基于上述定义，SVM 的学习问题可以表示为以下形式： ${\max }_{\mathbf{w},b}\gamma$ $\text{s.t.}{y}_i\frac{{\mathbf{w}}^T{\mathbf{x}}_i+b}{\Vert \mathbf{w}\Vert }\ge \gamma \text{对于所有 }i=1,\dots ,N$

这是一个带约束的优化问题。但这个形式有些复杂，因为目标函数和约束条件中都包含 $\Vert \mathbf{w}\Vert$，导致它们是非线性的且不方便求解。

2.5 SVM 优化问题的简化与标准化

为了简化问题，我们利用几何间隔的尺度不变性。我们可以固定函数间隔 $\hat{\gamma }$ 的某个值，例如，令最小函数间隔为 1。 ${\min }_{i=1,\dots ,N}{y}_i({\mathbf{w}}^T{\mathbf{x}}_i+b)=1$ 解释：

• 由于函数间隔 ${\hat{\gamma }}_i=y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)$ 可以通过缩放 $\mathbf{w}$ 和 $b$ 来任意改变，我们可以选择一个特定的缩放因子，使得距离超平面最近的那些点（被称为支持向量）的函数间隔恰好为 1。
• 一旦我们固定了最小函数间隔为 1，那么对于所有样本 $i$，都有 $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1$。
• 在这种标准化下，整个数据集的几何间隔 $\gamma$ 就变成了： $\gamma ={\min }_{i=1,\dots ,N}{y}_i\frac{{\mathbf{w}}^T{\mathbf{x}}_i+b}{\Vert \mathbf{w}\Vert }=\frac{1}{\Vert \mathbf{w}\Vert }{\min }_{i=1,\dots ,N}{y}_i({\mathbf{w}}^T{\mathbf{x}}_i+b)=\frac{1}{\Vert \mathbf{w}\Vert }\cdot 1=\frac{1}{\Vert \mathbf{w}\Vert }$
• 所以，最大化几何间隔 $\gamma$ 等价于最大化 $\frac{1}{\Vert \mathbf{w}\Vert }$，这又等价于最小化 $\Vert \mathbf{w}\Vert$。
• 为了方便求导和进行二次规划，我们通常最小化 $\Vert \mathbf{w}{\Vert }^2$ 或 $1/2\Vert \mathbf{w}{\Vert }^2$（乘以 1/2 不改变最优解，但方便求导）。

因此，线性可分支持向量机的学习问题最终被转化为以下凸二次规划 (Convex Quadratic Programming) 问题：

${\min }_{\mathbf{w},b}\frac{1}{2}\Vert \mathbf{w}{\Vert }^2$ $\text{s.t.}{y}_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1\text{对于所有 }i=1,\dots ,N$ 这是一个标准形式，可以利用现有的优化工具（如拉格朗日乘子法和对偶问题）进行求解。

3. 最优解的可识别性 (Uniqueness of the Optimal Solution)

“最优解具有可识别性”意味着，通过上述优化问题，我们能够唯一地确定最优的超平面参数 $({\mathbf{w}}^{\ast },b^{\ast })$。这与感知机形成鲜明对比，感知机可能找到无数个解。

让我们来分析为什么在标准化（即 ${\min }_i{y}_i({\mathbf{w}}^T{\mathbf{x}}_i+b)=1$）之后，最优解 $({\mathbf{w}}^{\ast },b^{\ast })$ 是可识别的。

3.1 超平面的非唯一性与参数的非唯一性

首先要明确的是，一个超平面 ${\mathbf{w}}^T\mathbf{x}+b=0$ 是由其法向量方向和与原点的距离决定的。如果我们用 $(c\mathbf{w},cb)$ 来代替 $(\mathbf{w},b)$（其中 $c\ne 0$），那么 $c{\mathbf{w}}^T\mathbf{x}+cb=0$ 仍然定义的是同一个超平面。 因此，仅仅通过定义超平面，参数 $(\mathbf{w},b)$ 本身不是唯一的。

3.2 标准化如何带来可识别性

在 SVM 的优化问题中，我们引入了约束条件： $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1$ 并且，在最优解处，至少对于那些位于间隔边界上的点（支持向量），这个等号是成立的： $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)=1\text{对于支持向量}$ 这意味着最小函数间隔被强制设定为 1。

• 对于权重向量 $\mathbf{w}$ 的唯一性： 我们最小化的目标函数是 $f(\mathbf{w})=\frac{1}{2}\Vert \mathbf{w}{\Vert }^2=\frac{1}{2}{\mathbf{w}}^T\mathbf{w}$。 这个目标函数 $f(\mathbf{w})$ 是一个严格凸函数 (Strictly Convex Function)。 解释：一个函数 $f(\mathbf{w})$ 是严格凸函数，意味着对于任意两个不同的点 ${\mathbf{w}}_1,{\mathbf{w}}_2$ 和 $0<\lambda <1$，有 $f(\lambda {\mathbf{w}}_1+(1-\lambda ){\mathbf{w}}_2)<\lambda f({\mathbf{w}}_1)+(1-\lambda )f({\mathbf{w}}_2)$。几何上，连接函数图像上两点的线段，除了端点外，都在函数图像的上方。 重要性质：对于一个在凸可行域上的严格凸函数，如果存在最优解，那么这个最优解是唯一的。 我们的约束 $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1$ 定义的是一个凸集。因此，在这些线性约束下，严格凸函数 $1/2\Vert \mathbf{w}{\Vert }^2$ 的最小值所对应的 ${\mathbf{w}}^{\ast }$ 是唯一确定的。
• 对于偏置项 $b$ 的唯一性： 一旦 ${\mathbf{w}}^{\ast }$ 确定了，偏置项 $b^{\ast }$ 也会被唯一确定。 这是因为 $b^{\ast }$ 必须使得至少一个支持向量恰好落在其对应的间隔边界上。 例如，对于任何一个支持向量 $({\mathbf{x}}_S,y_S)$，我们有 $y_S({\mathbf{w}}^{\ast T}{\mathbf{x}}_S+b^{\ast })=1$。 这可以写成 ${\mathbf{w}}^{\ast T}{\mathbf{x}}_S+b^{\ast }=y_S$。 因此，$b^{\ast }=y_S-{\mathbf{w}}^{\ast T}{\mathbf{x}}_S$。 由于 ${\mathbf{w}}^{\ast }$ 是唯一的，且支持向量 ${\mathbf{x}}_S$ 和 $y_S$ 是数据点，因此 $b^{\ast }$ 也是唯一确定的。 （实际上，在求解对偶问题时，$b^{\ast }$ 可以通过选择任意支持向量来计算，所有支持向量计算出的 $b^{\ast }$ 应该相同。）

3.3 可识别性的意义

通过上述标准化和优化，我们确保了：

1. 最优的超平面本身是唯一的。
2. 定义这个唯一超平面的参数 $({\mathbf{w}}^{\ast },b^{\ast })$ 也是唯一的。 这种可识别性使得 SVM 的解具有很好的稳定性，并且在理论上更具说服力。它表明 SVM 找到的决策边界不仅仅是“一个”分类器，而是**“最好”的那个**，因为它能够最大化数据点到决策边界的间隔。

4. 为什么我们可以利用几何间隔的尺度不变性，固定函数间隔 $\hat{\gamma }$ 为某个值？

在前面的讨论中，我们定义了两种间隔：

• 函数间隔 (Functional Margin)：${\hat{\gamma }}_i=y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)$
• 几何间隔 (Geometric Margin)：${\gamma }_i=\frac{y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)}{\Vert \mathbf{w}\Vert }=\frac{{\hat{\gamma }}_i}{\Vert \mathbf{w}\Vert }$

我们知道，SVM 的核心目标是最大化几何间隔 $\gamma ={\min }_i{\gamma }_i$。现在我们来深入理解，为什么在最大化几何间隔时，我们可以“顺便”地将最小函数间隔 $\hat{\gamma }={\min }_i{\hat{\gamma }}_i$ 固定为 1。

4.1 超平面的定义与参数的尺度

一个超平面在 $d$ 维空间中由方程 ${\mathbf{w}}^T\mathbf{x}+b=0$ 定义。 考虑以下情况： 假设我们有一个超平面，由参数 $(\mathbf{w},b)$ 定义。 现在，我们引入一个任意的正数 $c>0$。我们用新的参数 $({\mathbf{w}}^{\prime },b^{\prime })=(c\mathbf{w},cb)$ 来代替原来的参数。

让我们看看这会如何影响超平面以及两种间隔：

• 超平面本身： 新的超平面方程为 ${\mathbf{w}}^{\prime T}\mathbf{x}+b^{\prime }=0$，即 $(c\mathbf{w}{)}^T\mathbf{x}+cb=0$。 这等价于 $c({\mathbf{w}}^T\mathbf{x}+b)=0$。 由于 $c>0$，所以这个方程与 ${\mathbf{w}}^T\mathbf{x}+b=0$ 是完全等价的。它们定义的是空间中的同一个超平面。 结论：超平面本身与其定义参数 $(\mathbf{w},b)$ 的绝对尺度无关，只与它们的相对比例有关。例如，超平面 $x+y+1=0$ 和 $2x+2y+2=0$ 是同一个超平面。

• 函数间隔： 对于新的参数 $({\mathbf{w}}^{\prime },b^{\prime })$, 样本 ${\mathbf{x}}_i$ 的函数间隔为： ${\hat{\gamma }}_i^{\prime }=y_i({\mathbf{w}}^{\prime T}{\mathbf{x}}_i+b^{\prime })=y_i(c{\mathbf{w}}^T{\mathbf{x}}_i+cb)=c\cdot y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)=c{\hat{\gamma }}_i$ 结论：函数间隔是依赖于参数尺度的。如果你将 $\mathbf{w}$ 和 $b$ 乘以 $c$，函数间隔也会被乘以 $c$。因此，如果我们将所有函数间隔都乘以一个常数，超平面本身并没有改变。

• 几何间隔： 对于新的参数 $({\mathbf{w}}^{\prime },b^{\prime })$, 样本 ${\mathbf{x}}_i$ 的几何间隔为： ${\gamma }_i^{\prime }=\frac{{\hat{\gamma }}_i^{\prime }}{\Vert {\mathbf{w}}^{\prime }\Vert }=\frac{c{\hat{\gamma }}_i}{\Vert c\mathbf{w}\Vert }$ 因为 $\Vert c\mathbf{w}\Vert =|c|\Vert \mathbf{w}\Vert$，且我们假设 $c>0$，所以 $\Vert c\mathbf{w}\Vert =c\Vert \mathbf{w}\Vert$。 ${\gamma }_i^{\prime }=\frac{c{\hat{\gamma }}_i}{c\Vert \mathbf{w}\Vert }=\frac{{\hat{\gamma }}_i}{\Vert \mathbf{w}\Vert }={\gamma }_i$ 结论：几何间隔是不依赖于参数尺度的。无论我们将 $\mathbf{w}$ 和 $b$ 缩放多少倍（只要是正数），几何间隔保持不变。这是它被称为“几何”间隔的根本原因，因为它代表了真实的几何距离。

4.2 为什么可以固定最小函数间隔为 1？

由于几何间隔的尺度不变性，我们在优化时拥有一个很大的自由度：我们可以任意选择参数 $(\mathbf{w},b)$ 的具体数值，只要它们定义了同一个最优超平面即可。

我们的目标是最大化整个数据集的最小几何间隔 $\gamma ={\min }_i{\gamma }_i$。 我们知道 $\gamma =\frac{\hat{\gamma }}{\Vert \mathbf{w}\Vert }$，其中 $\hat{\gamma }={\min }_i{\hat{\gamma }}_i$ 是最小函数间隔。

因为几何间隔与参数尺度无关，我们可以选择任何一种标准化来固定参数的尺度。最方便、最简单的标准化方式就是固定最小函数间隔 $\hat{\gamma }$ 为一个特定的正数值。

• 如果我们选择令 $\hat{\gamma }=1$： 这意味着我们将参数 $(\mathbf{w},b)$ 进行缩放，使得所有样本中距离超平面最近的那个点（或那几个点，即支持向量）的函数间隔恰好为 1。 也就是说，对于所有训练样本 $i$，我们强制要求： $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1$ 并且对于至少一个样本（支持向量），等号成立。

• 这种标准化如何简化优化问题？ 在这种情况下，整个数据集的最小几何间隔 $\gamma$ 就可以表示为： $\gamma =\frac{{\min }_i{y}_i({\mathbf{w}}^T{\mathbf{x}}_i+b)}{\Vert \mathbf{w}\Vert }=\frac{1}{\Vert \mathbf{w}\Vert }\cdot \left({\min }_i{y}_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\right)$ 由于我们已经通过缩放将 ${\min }_i{y}_i({\mathbf{w}}^T{\mathbf{x}}_i+b)$ 固定为 1，那么： $\gamma =\frac{1}{\Vert \mathbf{w}\Vert }$ 因此，最大化几何间隔 $\gamma$ 就等价于最大化 $\frac{1}{\Vert \mathbf{w}\Vert }$，这又等价于最小化 $\Vert \mathbf{w}\Vert$。 为了数学上的方便，我们通常最小化 $\Vert \mathbf{w}{\Vert }^2$ 或 $\frac{1}{2}\Vert \mathbf{w}{\Vert }^2$（因为目标函数变为二次型，更方便求导，且不改变最优解的位置）。

结论： 正是因为几何间隔对参数 $(\mathbf{w},b)$ 的尺度变化具有不变性，我们才拥有了自由选择一个特定尺度的权利。选择将最小函数间隔固定为 1（即 $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1$）是一种最简洁、最常用的标准化方式，它将原本复杂的目标函数 $\max \gamma$ 转化为简单的 $\min \frac{1}{2}\Vert \mathbf{w}{\Vert }^2$，同时保留了所有约束条件，使得优化问题变得易于处理和求解。

5. 支持向量机的学习问题是凸优化问题吗？

答案是：是的，支持向量机的学习问题是一个典型的凸优化问题。

一个优化问题被称为凸优化问题，必须满足以下两个条件：

1. 目标函数 (Objective Function) 是凸函数。
2. 可行域 (Feasible Set) 是一个凸集。

我们来逐一验证 SVM 的学习问题（标准形式）： ${\min }_{\mathbf{w},b}\frac{1}{2}\Vert \mathbf{w}{\Vert }^2$ $\text{s.t.}{y}_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1\text{对于所有 }i=1,\dots ,N$ 其中，优化变量是 $\mathbf{w}$ 和 $b$。我们可以将它们看作一个更大的向量 $\mathbf{\theta }=(\mathbf{w},b{)}^T$。

5.1 目标函数是凸函数吗？

目标函数是 $f(\mathbf{w},b)=\frac{1}{2}\Vert \mathbf{w}{\Vert }^2=\frac{1}{2}{\mathbf{w}}^T\mathbf{w}$。 解释：

• 这个函数是一个二次函数，其图像在多维空间中是一个开口向上的“碗”形（抛物面）。这种形状的函数是典型的凸函数。
• 更严格地，我们可以通过计算其海森矩阵 (Hessian Matrix) 来验证。目标函数只依赖于 $\mathbf{w}$，不依赖于 $b$。 对于 $f(\mathbf{w})=\frac{1}{2}{\mathbf{w}}^T\mathbf{w}$： 其一阶导数（梯度）是 ${\nabla }_{\mathbf{w}}f(\mathbf{w})=\mathbf{w}$。 其二阶导数（Hessian 矩阵）是 ${\nabla }_{\mathbf{w}}^{2}f(\mathbf{w})=\mathbf{I}$ (单位矩阵)。
• 单位矩阵 $\mathbf{I}$ 是一个正定矩阵（所有对角线元素为 1，非对角线元素为 0；所有特征值都为 1，因此都大于 0）。
• 结论：如果一个函数的 Hessian 矩阵在整个定义域上都是正定（或半正定）的，那么这个函数就是严格凸（或凸）的。因此，目标函数 $\frac{1}{2}\Vert \mathbf{w}{\Vert }^2$ 是一个严格凸函数。

5.2 可行域是凸集吗？

可行域是由所有约束条件共同定义的区域。在这里，有 $N$ 个线性不等式约束： $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1\text{对于所有 }i=1,\dots ,N$ 我们可以将每个约束重新写成 $g_i(\mathbf{w},b)\le 0$ 的标准形式（对于最小化问题）： $1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\le 0$ 解释：

• 每个约束函数 $g_i(\mathbf{w},b)=1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)$ 都是关于 $\mathbf{w}$ 和 $b$ 的线性函数。 例如，如果 $y_i=1$，约束是 $1-({\mathbf{w}}^T{\mathbf{x}}_i+b)\le 0$。 如果 $y_i=-1$，约束是 $1+({\mathbf{w}}^T{\mathbf{x}}_i+b)\le 0$。
• 线性函数既是凸函数，也是凹函数。
• 重要性质：一个由凸不等式约束（$g_i(\mathbf{\theta })\le 0$）和线性等式约束（$h_j(\mathbf{\theta })=0$）定义的集合是一个凸集。
• 每个线性不等式约束 $1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\le 0$ 定义了一个半空间 (Half-space)。半空间是一个凸集。
• 凸集的交集仍然是凸集。可行域是所有这 $N$ 个半空间的交集。
• 结论：SVM 的可行域是一个凸集。

5.3 最终结论：凸优化问题

由于 SVM 的目标函数是严格凸函数，并且可行域是一个凸集，因此，SVM 的学习问题是一个凸优化问题。

5.4 凸优化问题的重要性

凸优化问题的性质在机器学习中极其重要：

1. 全局最优解的保证：对于凸优化问题，任何局部最优解都是全局最优解。这意味着我们不需要担心算法陷入局部最优，只要能找到一个满足 KKT 条件的点，它就是全局最优解。
2. 高效的求解算法：存在大量成熟、高效且收敛性有保证的算法（如二次规划、内点法等）可以用于求解凸优化问题。
3. 唯一性：由于目标函数是严格凸的（如 $\frac{1}{2}\Vert \mathbf{w}{\Vert }^2$），它在凸可行域上的最小值是唯一的。这再次印证了我们在上一节讨论的 SVM 最优解的可识别性。