为何要分解矩阵?
在深入数学细节之前,我们先建立一个直观的认识。在机器学习中,矩阵通常代表着数据或一种变换。例如,一个用户-物品评分矩阵,或者一个将输入向量变换到输出向量的线性算子。奇异值分解的核心思想是,任何复杂的线性变换(由矩阵 A 代表)都可以被拆解为三个基本、更易于理解的连续操作:
- 一次 旋转或反射。
- 一次沿着坐标轴的 缩放。
- 另一次 旋转或反射。
SVD的强大之处在于,它保证了任何矩阵都存在这样一种分解方式,并为我们揭示了矩阵内在的、最重要的“结构信息”。
一、奇异值分解的定义与基本定理
1.1 定义与符号约定(对应定义15.1)
我们首先严格地定义奇异值分解。
对于任意一个给定的 实矩阵 ,它的奇异值分解是指存在一个分解式,形如:
这里的每个组成部分都有明确的身份和性质:
- : 我们要分解的目标矩阵,维度为 。
- : 一个 的 正交矩阵(Orthogonal Matrix)。它的列向量 被称为 左奇异向量。
- “正交”意味着 的所有列向量彼此正交且长度为1(标准正交基),这使得 ( 是 阶单位矩阵)。从几何上看, 代表了一个不改变向量长度和夹角的旋转或反射操作。
- : 一个 的 正交矩阵。它的列向量 被称为 右奇异向量。
- 同样,“正交”意味着 。从几何上看, 也代表了一个旋转或反射操作。注意,在分解式中我们使用的是 。
- : 一个 的 矩形对角矩阵(Rectangular Diagonal Matrix)。它的特殊之处在于,只有主对角线上的元素可能非零,其余元素都为0。
- 这些对角线上的元素 被称为 奇异值,其中 。
- 按照约定,这些奇异值是非负的,并且是降序排列的:。
1.2 核心定理:存在性与构造性证明
定理 15.1:
若 为一个 实矩阵,则 的奇异值分解 存在。
这个定理的证明是构造性的,也就是说,我们通过一步步地找出 来证明它们的存在性。这正是理解SVD计算原理的关键。为方便讨论,我们不妨假设 (若 ,证明逻辑完全对称,只需从 出发即可)。
证明步骤:
第一步:构造 和
这一步的核心技巧是,我们不直接处理可能非方阵、非对称的 ,而是构造一个与之相关且性质优良的矩阵。这个矩阵就是 。
-
构造辅助矩阵:我们计算 。
-
是 矩阵, 是 矩阵,所以 是一个 的 方阵。
-
更重要的是, 是 对称的,因为 。
-
并且, 是 半正定的。这意味着对于任意非零向量 ,都有 。这一点从如下的公式(15.3)的推导可以看出:
这个性质保证了 的所有特征值都是非负的。
-
-
对 进行特征值分解:
-
根据谱定理,任何实对称矩阵都可以被正交对角化。因此,存在一个 的正交矩阵 和一个对角矩阵 ,使得:
-
矩阵 的列向量 就是 的标准正交特征向量。这便是我们SVD中所需要的 。
-
对角矩阵 的对角元 就是 的特征值。由于 是半正定的,我们知道所有 。我们可以将它们降序排列。
-
-
定义奇异值:
-
我们定义矩阵 的 奇异值 为其特征值 的平方根:
-
将这些奇异值降序排列 ,并用它们构建 的矩形对角矩阵 。当 时, 的形式如下:
-
至此,我们已经成功构造出了 和 。
-
第二步:构造
现在,我们有了 和 ,需要根据关系式 来找出 。将关系式两边同时右乘 ,得到:
我们把这个矩阵方程展开,逐列来看。设 的秩为 ,即 有 个非零特征值,因此有 个非零奇异值 ,而 。
-
定义 的前 列:
-
对于 ,上面的矩阵方程的第 列是:
-
由于 ,我们可以定义 为:
这给了我们 的前 个列向量。
-
-
证明这 列是标准正交的:我们需要证明 ( 当 时为1,否则为0)。
- 由于 的列向量 是标准正交的,所以 。
- 当 时,上式变为 。
- 当 时,上式变为 。
- 这就证明了 构成了 空间中的一个标准正交向量集。
-
构造 的剩余 列:
- 我们已经有了 个标准正交的 维向量。如果 ,这 个向量张成的是 的一个子空间。
- 我们可以使用如格拉姆-施密特(Gram-Schmidt)正交化等方法,找到另外 个单位向量 ,使得它们与 正交,并且彼此也正交。
- 这样,我们就得到了完整的 个标准正交向量,将它们作为列,构成了一个 的正交矩阵 。
第三步:验证
我们已经构造好了 。现在只需验证它们相乘的结果是否确实是 。我们来计算 :
为了证明这个和等于 ,我们可以证明它们作用在任意向量 上结果相同。
由于 是 的一组基,上述等式对所有基向量成立,意味着对任意向量都成立。因此,我们证明了 。
证明完毕。 这个构造过程不仅证明了SVD的存在性,也为我们提供了计算它的蓝图。
二、奇异值分解的不同形式
根据实际需求,SVD有几种不同的变体。
2.1 完全奇异值分解(Full SVD)
这就是我们刚刚证明和定义的标准形式:。 和 都是满秩的方阵, 的维度与 完全相同,包含了大量的零。
2.2 紧凑奇异值分解(Compact SVD,对应定义15.2)
在实际应用中,奇异值为零的部分通常是冗余信息。紧凑SVD就是去除这些冗余部分。设矩阵 的秩为 (即有 个非零奇异值)。
- : 是一个 的对角方阵,仅包含 个非零奇异值 。
- : 取完全SVD中 的前 列(即 ),构成一个 的矩阵。
- : 取完全SVD中 的前 列(即 ),构成一个 的矩阵。 则是 维度。
为什么可以这样做? 回顾完全SVD的乘法过程 ,我们会发现 中第 列到第 列,以及 中第 列到第 列,都将与 中的零元素相乘。因此,这些列对最终结果 没有任何贡献。紧凑SVD正是去除了这些无贡献的部分,使得存储和计算更高效。
2.3 截断奇异值分解(Truncated SVD)
这是SVD在机器学习中应用最广泛的形式。它不仅去除了零奇异值部分,还进一步舍弃了那些值很小的奇异值。我们选择一个远小于秩 的数 ,只保留前 个最大的奇异值。
- : 是一个 的对角方阵,包含前 个最大的奇异值。
- : 取 的前 列,构成 矩阵。
- : 取 的前 列,构成 矩阵。
这里的关键是 约等于()。 是原矩阵 的一个 低秩近似。后续我们会学到(对应书15.3节),截断SVD是在所有秩为 的矩阵中,对原矩阵 的最优近似。这正是PCA降维、数据压缩和去噪的理论基础。
三、几何解释
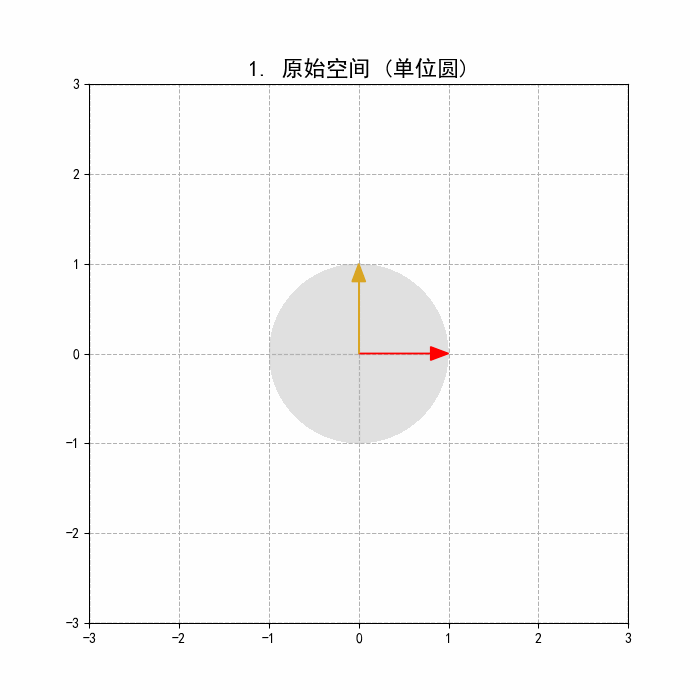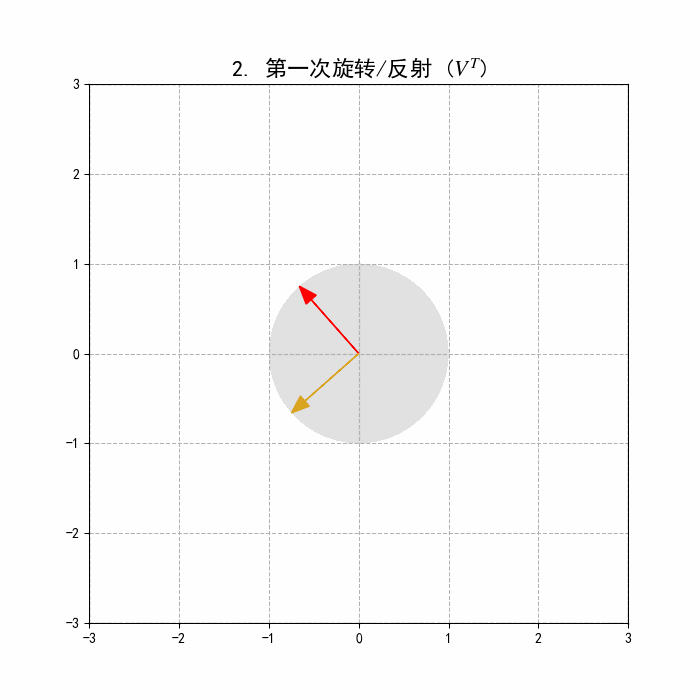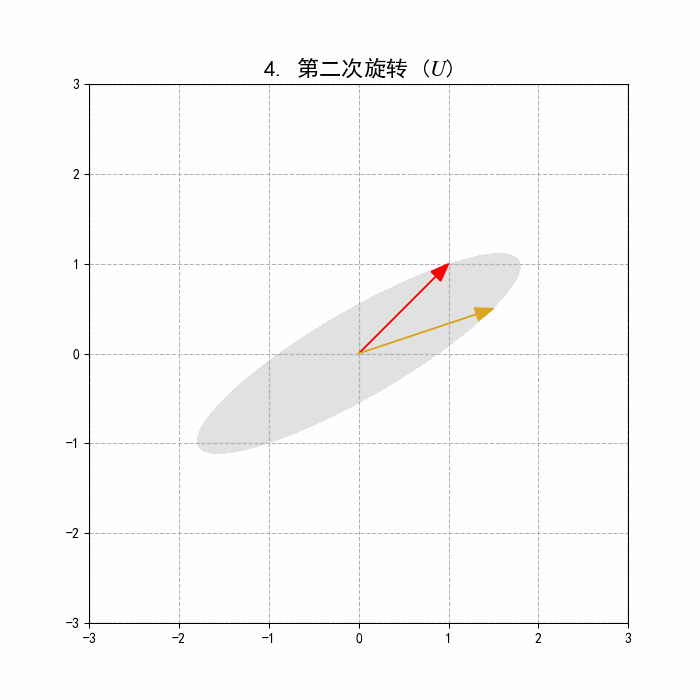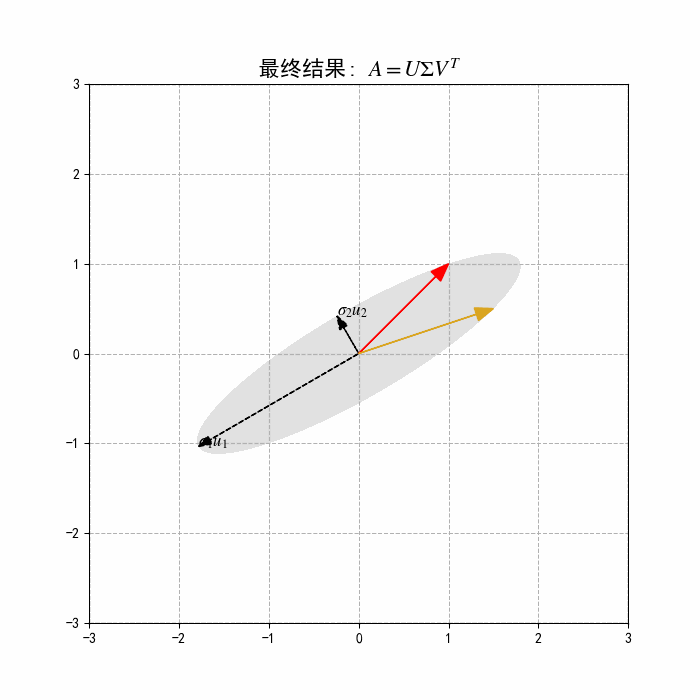
一个 的矩阵 可以看作一个从 维空间 到 维空间 的线性变换 。
SVD分解 告诉我们,这个看似复杂的变换 可以分解为三步:
考虑一个向量 经过变换 的过程:
-
第一步: (输入空间的坐标系旋转/反射)
- 的列向量 构成 空间的一组新的标准正交基。
- 计算 的过程,实际上是将向量 从标准的坐标系 投影到这个由 的列向量定义的 新坐标系 上,得到新的坐标。可以理解为对输入空间进行了一次旋转或反射,使得基准坐标轴与 对齐。
-
第二步: (沿新坐标轴的缩放)
- 是一个矩形对角矩阵。它将上一步得到的新坐标向量的每一个分量,沿着新的坐标轴(即 方向)进行缩放,缩放比例就是对应的奇异值 。
- 如果 很大,说明在这个方向上的拉伸很显著。
- 如果 很小,说明在这个方向上的信息被压缩了。
- 如果 (对于 ),说明这个维度直接被“压扁”了,其信息完全丢失。
- 经过这一步,我们得到一个在 维空间中的向量(因为 是 的),但它仍然是用一个中间坐标系来表示的。
-
第三步: (输出空间的坐标系旋转/反射)
- 的列向量 构成了输出空间 的一组新的标准正交基。
- 将上一步得到的缩放后的向量乘以 ,相当于将这个向量从中间坐标系(与 关联)转换回 的标准坐标系中。这可以理解为对输出空间进行了一次旋转或反射。
一个经典的类比: 想象在二维空间中,将一个单位圆上的所有点进行线性变换。
- 找到了最适合拉伸的“主轴方向”,并将圆旋转,使主轴与标准坐标轴对齐。
- 沿着对齐后的坐标轴进行不同程度的拉伸或压缩,将单位圆变成一个椭圆。
- 再将这个对齐的椭圆旋转到它在目标空间中的最终位置。
所以,SVD的几何本质就是:任何线性变换都可以看作是“旋转-缩放-再旋转”的组合。奇异值 就是缩放的比例,而左右奇异向量构成的正交矩阵 和 则定义了这两个旋转。
四、主要性质
SVD的代数结构引出了一些非常重要的性质。
(1) SVD与 和 的特征值分解的深刻联系
这一点在我们证明SVD存在性时已经用到了,这里我们正式地总结一下。
-
对于 :
这正是 的特征值分解。 是其特征向量矩阵,而对角矩阵 (这是一个 的方阵)的对角元是 ,即 的特征值。
-
对于 :
这正是 的特征值分解。 是其特征向量矩阵,而对角矩阵 (这是一个 的方阵)的对角元是 (如果 ),即 的特征值。
结论:矩阵 的奇异值是 和 的非零特征值的平方根。 的右奇异向量是 的特征向量, 的左奇异向量是 的特征向量。这是计算SVD的标准算法基础。
(2) 左、右奇异向量与奇异值之间的关系
从 可以直接推导出左右奇异向量之间的桥梁关系。
-
右乘 得到 。比较两边矩阵的第 列:
这表明,右奇异向量 经过矩阵 变换后,会恰好落在其对应的左奇异向量 的方向上,并且长度被缩放了 倍。
-
类似地,从 右乘 得到 。比较两边矩阵的第 列:
这表明,左奇异向量 经过矩阵 变换后,会恰好落在其对应的右奇异向量 的方向上,长度同样被缩放了 倍。
这两个关系式完美地诠释了 和 分别是 的输出空间和输入空间中的“特殊基向量”。
后续,我们学习一下奇异值分解的求解方法奇异值分解(二):计算方法与例题。