非线性支持向量机

非线性支持向量机 (Non-linear Support Vector Machines)

1. 为什么需要非线性支持向量机？

1.1 线性支持向量机的局限性回顾

在之前的学习中，我们了解到线性支持向量机（无论是硬间隔还是软间隔）都是为了找到一个超平面来分离不同类别的样本。它非常高效，并且在数据线性可分时能够找到最优的决策边界（最大间隔超平面）。

其核心优化问题，无论是原始形式还是对偶形式，都依赖于数据在原始输入空间中的线性可分性： 原始问题：

${\min }_{\mathbf{w},b,\mathbf{\xi }}\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C{\sum }_{i=1}^N{\xi }_i$ $\text{s.t.}{y}_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1-{\xi }_i,{\xi }_i\ge 0\text{对于所有 }i=1,\dots ,N$

对偶问题：

${\max }_{\mathbf{\alpha }}{\sum }_{i=1}^N{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j({\mathbf{x}}_i^T{\mathbf{x}}_j)$

$\text{s.t.}{\sum }_{i=1}^N{\alpha }_i{y}_i=0,0\le {\alpha }_i\le C\text{对于所有 }i=1,\dots ,N$

解释：这些问题都是在原始的输入空间 $\mathcal{X}$ 中寻找一个线性决策边界。

1.2 现实世界中的非线性可分数据

然而，在现实世界中，很多数据集并非线性可分。例如：

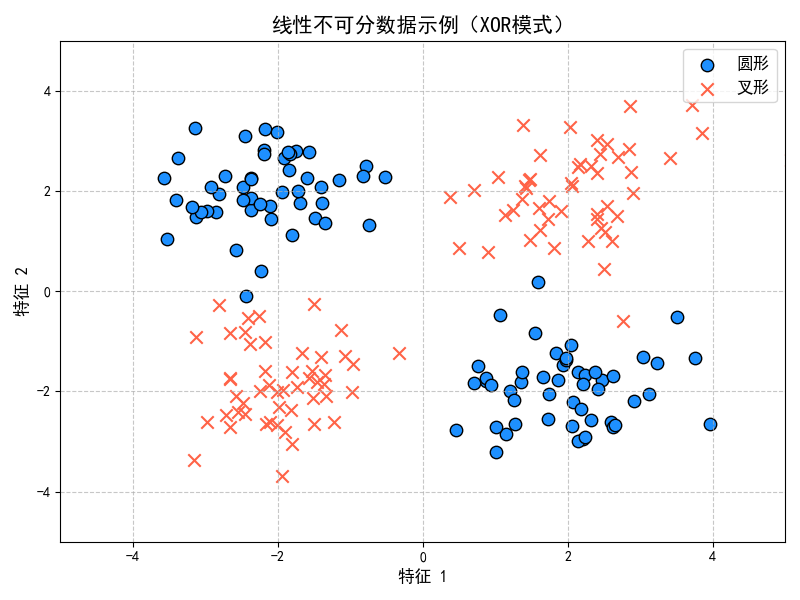
• 圆形样本（O）和叉叉样本（X）在二维平面上无法用一条直线完美分开。正负类样本在空间中呈环形或交错分布。
• 如果强行用线性 SVM 去分类，模型性能会非常差，甚至无法收敛到有效解（对于硬间隔 SVM）。

非线性支持向量机的提出，正是为了解决这种线性不可分的问题。

2. 映射到高维特征空间

非线性 SVM 的核心思想是： 如果数据在原始输入空间 $\mathcal{X}$ 中是线性不可分的，那么我们尝试将数据点从原始空间 $\mathcal{X}$ 映射到一个更高维的（甚至可能是无限维的）特征空间 $\mathcal{H}$。在新的特征空间 $\mathcal{H}$ 中，数据点可能会变得线性可分。

• 原始空间 (Input Space)：通常是欧几里得空间 ${\mathbb{R}}^d$，例如 $\mathbf{x}=(x^{(1)},x^{(2)}{)}^T$ 所在的二维空间。
• 特征空间 (Feature Space)：我们映射到的新空间，通常用 $\mathcal{H}$ 表示。它的维度可能远高于原始空间，甚至可能是无限维。
• 映射函数 $\Phi (\mathbf{x})$：这个函数负责将原始空间中的数据点 $\mathbf{x}$ 转换到特征空间中的新表示 $\Phi (\mathbf{x})$。 $\Phi :\mathcal{X}\to \mathcal{H}$ 对于原始空间中的一个样本 ${\mathbf{x}}_i$，经过映射后变成 $\Phi ({\mathbf{x}}_i)$。

在特征空间 $\mathcal{H}$ 中构建线性分类器： 一旦数据被映射到特征空间 $\mathcal{H}$，我们就假设在这个新的高维空间中，数据点是线性可分的。我们仍然使用线性 SVM 的方法，在新空间中寻找一个线性超平面： ${\mathbf{w}}_{\mathcal{H}}^T\Phi (\mathbf{x})+b=0$ 这里的 ${\mathbf{w}}_{\mathcal{H}}$ 是特征空间 $\mathcal{H}$ 中的权重向量。

直观理解： 想象一下你有一堆硬币，有些正面朝上，有些反面朝上，它们在桌面上是混合的（线性不可分）。但是如果你把它们都拿起来，正面的放在桌子上方 10 厘米处，反面的放在 0 厘米处，那么在“高度”这个新的维度上，它们就变得线性可分了。这就是从低维空间映射到高维空间的思想。

3. 核技巧

虽然将数据映射到高维空间听起来很有效，但它带来了两个主要问题：

1. 计算成本高昂：如果特征空间 $\mathcal{H}$ 的维度非常高，甚至无限维，显式地计算 $\Phi (\mathbf{x})$ 将变得极其耗时或不可能。
2. 具体形式未知：很多时候我们甚至不知道一个合适的映射函数 $\Phi (\mathbf{x})$ 具体长什么样子。

幸运的是，我们有一个巧妙的解决方案，这就是核技巧 (Kernel Trick)。

3.1 对偶问题中的内积

回顾线性 SVM 的对偶优化问题，你会发现所有涉及输入特征 ${\mathbf{x}}_i$ 的地方，都以 内积（点积） 的形式出现：$({\mathbf{x}}_i^T{\mathbf{x}}_j)$。

${\max }_{\mathbf{\alpha }}{\sum }_{i=1}^N{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j({\mathbf{x}}_i^T{\mathbf{x}}_j)$

$\text{s.t.}{\sum }_{i=1}^N{\alpha }_i{y}_i=0,0\le {\alpha }_i\le C$

如果我们把数据映射到特征空间 $\mathcal{H}$，那么原始问题中的 ${\mathbf{x}}_i$ 就会被替换为 $\Phi ({\mathbf{x}}_i)$。因此，在对偶问题中，所有的内积形式都会变为：

$\Phi ({\mathbf{x}}_i{)}^T\Phi ({\mathbf{x}}_j)$

3.2 核函数的定义

核函数 (Kernel Function) 的核心思想是：我们不需要显式地知道映射函数 $\Phi (\mathbf{x})$，也不需要计算高维的 $\Phi (\mathbf{x})$。我们只需要找到一个函数 $K({\mathbf{x}}_i,{\mathbf{x}}_j)$，使得它能够直接计算出在高维特征空间中的内积：

$K({\mathbf{x}}_i,{\mathbf{x}}_j)=\Phi ({\mathbf{x}}_i{)}^T\Phi ({\mathbf{x}}_j)$

通过这个替换，我们就可以在不对数据进行显式高维映射的情况下，直接在原始空间中计算出高维空间中的内积。这就像是“只在幕后”进行高维映射，而不需要真正地“走到台前”。

非线性 SVM 的对偶问题：

${\max }_{\mathbf{\alpha }}{\sum }_{i=1}^N{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K({\mathbf{x}}_i,{\mathbf{x}}_j)$ $\text{s.t.}{\sum }_{i=1}^N{\alpha }_i{y}_i=0,0\le {\alpha }_i\le C$

决策函数： 最终的决策函数也会涉及到内积。根据 KKT 条件，最优的权重向量 ${\mathbf{w}}^{\ast }$ 可以表示为支持向量的线性组合： ${\mathbf{w}}^{\ast }={\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_i\Phi ({\mathbf{x}}_i)$ 那么对于一个新的输入 $\mathbf{x}$，分类决策函数为： $f(\mathbf{x})=\text{sign}({\mathbf{w}}^{\ast T}\Phi (\mathbf{x})+b^{\ast })=\text{sign}\left({\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_i\Phi ({\mathbf{x}}_i{)}^T\Phi (\mathbf{x})+b^{\ast }\right)$ 利用核函数： $f(\mathbf{x})=\text{sign}\left({\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_{i}K({\mathbf{x}}_i,\mathbf{x})+b^{\ast }\right)$ 解释：整个 SVM 的训练和预测过程都巧妙地避开了对 $\Phi (\mathbf{x})$ 的显式计算。

4. 希尔伯特空间 (Hilbert Space)

4.1 什么是希尔伯特空间？

希尔伯特空间 (Hilbert Space) 是一种在数学中，尤其是泛函分析中使用的抽象概念，它是欧几里得空间的推广。

定义：一个希尔伯特空间是一个完备的内积空间。

• 内积空间 (Inner Product Space)：
  • 一个向量空间，其中定义了内积操作。内积接受两个向量，返回一个标量。
  • 内积满足：对称性、线性、正定性。
  • 内积允许我们定义 长度（范数） 和 角度 。例如，向量 $\mathbf{v}$ 的长度 $\Vert \mathbf{v}\Vert =\sqrt{⟨\mathbf{v},\mathbf{v}⟩}$。
  • 在有限维空间中，我们常用的点积 $\mathbf{a}\cdot \mathbf{b}={\mathbf{a}}^T\mathbf{b}$ 就是一种内积。
• 完备性 (Completeness)：
  • 指的是空间中所有柯西序列（Cauchy sequence）都收敛于该空间内的一个点。
  • 完备性保证了我们可以进行极限操作，这在分析和优化算法的收敛性时非常重要。它确保了在空间中进行逼近时，我们不会“跳出”空间。

4.2 希尔伯特空间在 SVM 中的作用

在 SVM 的语境中：

• 我们所说的特征空间 $\mathcal{H}$ 往往是一个希尔伯特空间（或被视为一个希尔伯特空间）。
• 映射函数 $\Phi (\mathbf{x})$ 将原始输入空间 $\mathcal{X}$ 中的点映射到这个特征空间 $\mathcal{H}$ 中。
• 核函数 $K({\mathbf{x}}_i,{\mathbf{x}}_j)$ 实际上就是特征空间 $\mathcal{H}$ 中的内积操作 $⟨\Phi ({\mathbf{x}}_i),\Phi ({\mathbf{x}}_j)⟩$。
• 通过在希尔伯特空间中进行计算，我们能够利用其丰富的几何性质（如距离和正交性），同时避免显式地处理可能无限维的向量。这种利用内积来规避高维计算的方法被称为 “表征定理 (Representer Theorem)” 的体现，它表明最优解可以表示为数据点的线性组合，而这个线性组合只需要内积。

5. 正定核 (Positive Definite Kernel)

并非所有的对称函数都可以作为核函数。一个函数 $K(\mathbf{x},\mathbf{z})$ 要成为一个合法的核函数，它必须满足特定的数学条件，即它必须是正定核 (Positive Definite Kernel)。

5.1 正定核的条件

一个函数 $K(\mathbf{x},\mathbf{z})$ 如果满足以下两个条件，则称其为正定核（或 Mercer 核）：

1. 对称性 (Symmetry)： $K(\mathbf{x},\mathbf{z})=K(\mathbf{z},\mathbf{x})$ 解释：这是因为内积操作本身就是对称的：$\Phi (\mathbf{x}{)}^T\Phi (\mathbf{z})=\Phi (\mathbf{z}{)}^T\Phi (\mathbf{x})$。

2. 半正定性 (Positive Semi-Definiteness) of the Gram Matrix： 对于任意有限个样本点 ${\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_m$ 和任意非零实数 $c_1,c_2,\dots ,c_m$，以下条件必须成立： ${\sum }_{i=1}^m{\sum }_{j=1}^m{c}_i{c}_{j}K({\mathbf{x}}_i,{\mathbf{x}}_j)\ge 0$ 解释：这个条件等价于说，由 $K({\mathbf{x}}_i,{\mathbf{x}}_j)$ 构成的 Gram 矩阵 $\mathbf{K}$ 必须是半正定矩阵。 Gram 矩阵 $\mathbf{K}$ 是一个 $m\times m$ 的矩阵，其第 $i$ 行第 $j$ 列的元素是 $K_{ij}=K({\mathbf{x}}_i,{\mathbf{x}}_j)$。

   半正定矩阵的直观意义： 如果一个矩阵 $\mathbf{K}$ 是半正定的，意味着它所对应的二次型 ${\mathbf{c}}^T\mathbf{Kc}$ 总是非负的。 这个条件是至关重要的，因为它保证了：

   • 存在一个隐式的映射 $\Phi$ 使得 $K({\mathbf{x}}_i,{\mathbf{x}}_j)=\Phi ({\mathbf{x}}_i{)}^T\Phi ({\mathbf{x}}_j)$。
   • 在特征空间中，任意向量的平方范数（长度的平方）是非负的： ${\Vert {\sum }_{i=1}^m{c}_i\Phi ({\mathbf{x}}_i)\Vert }^2=⟨{\sum }_{i=1}^m{c}_i\Phi ({\mathbf{x}}_i),{\sum }_{j=1}^m{c}_j\Phi ({\mathbf{x}}_j)⟩={\sum }_{i=1}^m{\sum }_{j=1}^m{c}_i{c}_j⟨\Phi ({\mathbf{x}}_i),\Phi ({\mathbf{x}}_j)⟩={\sum }_{i=1}^m{\sum }_{j=1}^m{c}_i{c}_{j}K({\mathbf{x}}_i,{\mathbf{x}}_j)\ge 0$ 这确保了特征空间是一个合法的欧几里得空间（或更广义的希尔伯特空间），其中可以进行距离和角度的计算。

5.2 Mercer 定理 (Mercer’s Theorem)

Mercer 定理提供了判断一个函数是否为正定核的充要条件： 一个对称函数 $K(\mathbf{x},\mathbf{z})$ 是核函数的充要条件是，对于任何有限个样本点，由它生成的 Gram 矩阵都是半正定的。 解释：这个定理非常重要，因为它使得我们无需显式构造 $\Phi (\mathbf{x})$ 就可以验证一个函数是否可以作为核函数。我们只需要检查它的对称性以及对应的 Gram 矩阵的半正定性。

6. 一个构造示例

我们来详细推导一个具体的例子，展示如何从一个核函数形式找到对应的映射函数 $\Phi (\mathbf{x})$，并验证它们之间的关系。

设原始输入空间是 ${\mathbb{R}}^2$，即 $\mathbf{x}=(x^{(1)},x^{(2)}{)}^T$ 和 $\mathbf{z}=(z^{(1)},z^{(2)}{)}^T$。 我们考察核函数 $K(\mathbf{x},\mathbf{z})=(\mathbf{x}\cdot \mathbf{z}{)}^2$。

步骤 1：展开核函数 $K(\mathbf{x},\mathbf{z})=(\mathbf{x}\cdot \mathbf{z}{)}^2=(x^{(1)}{z}^{(1)}+x^{(2)}{z}^{(2)}{)}^2$ 使用 $(A+B{)}^2=A^2+2AB+B^2$ 展开： $=(x^{(1)}{z}^{(1)}{)}^2+2(x^{(1)}{z}^{(1)})(x^{(2)}{z}^{(2)})+(x^{(2)}{z}^{(2)}{)}^2$ 重新排列项，将属于 $\mathbf{x}$ 的部分和属于 $\mathbf{z}$ 的部分组合在一起： $=(x^{(1)}{)}^2(z^{(1)}{)}^2+2x^{(1)}{x}^{(2)}{z}^{(1)}{z}^{(2)}+(x^{(2)}{)}^2(z^{(2)}{)}^2$

步骤 2：构造映射函数 $\Phi (\mathbf{x})$ 我们的目标是找到一个 $\Phi (\mathbf{x})$ 使得 $K(\mathbf{x},\mathbf{z})=\Phi (\mathbf{x})\cdot \Phi (\mathbf{z})$。 观察展开后的形式，它看起来像两个向量的点积。我们可以将它分解为两个向量的对应元素相乘再求和。

一种可能的映射 ${\Phi }_1(\mathbf{x})$ ： 令特征空间是 ${\mathbb{R}}^3$。 ${\Phi }_1(\mathbf{x})=((x^{(1)}{)}^2,\sqrt{2}{x}^{(1)}{x}^{(2)},(x^{(2)}{)}^2{)}^T$ 那么： ${\Phi }_1(\mathbf{z})=((z^{(1)}{)}^2,\sqrt{2}{z}^{(1)}{z}^{(2)},(z^{(2)}{)}^2{)}^T$ 现在计算它们的点积： ${\Phi }_1(\mathbf{x})\cdot {\Phi }_1(\mathbf{z})=(x^{(1)}{)}^2(z^{(1)}{)}^2+(\sqrt{2}{x}^{(1)}{x}^{(2)})(\sqrt{2}{z}^{(1)}{z}^{(2)})+(x^{(2)}{)}^2(z^{(2)}{)}^2$ $=(x^{(1)}{)}^2(z^{(1)}{)}^2+2x^{(1)}{x}^{(2)}{z}^{(1)}{z}^{(2)}+(x^{(2)}{)}^2(z^{(2)}{)}^2$ 这正是 $K(\mathbf{x},\mathbf{z})$ 的展开形式。 所以，这种映射是有效的。

**另一种可能的映射 ${\Phi }_2(\mathbf{x})$： 令特征空间是 ${\mathbb{R}}^4$。 我们可以将中间项 $2x^{(1)}{x}^{(2)}{z}^{(1)}{z}^{(2)}$ 拆开成两个对称项 $x^{(1)}{x}^{(2)}{z}^{(1)}{z}^{(2)}+x^{(2)}{x}^{(1)}{z}^{(2)}{z}^{(1)}$。 ${\Phi }_2(\mathbf{x})=((x^{(1)}{)}^2,x^{(1)}{x}^{(2)},x^{(2)}{x}^{(1)},(x^{(2)}{)}^2{)}^T$ 那么： ${\Phi }_2(\mathbf{z})=((z^{(1)}{)}^2,z^{(1)}{z}^{(2)},z^{(2)}{z}^{(1)},(z^{(2)}{)}^2{)}^T$ 计算它们的点积： ${\Phi }_2(\mathbf{x})\cdot {\Phi }_2(\mathbf{z})=(x^{(1)}{)}^2(z^{(1)}{)}^2+x^{(1)}{x}^{(2)}{z}^{(1)}{z}^{(2)}+x^{(2)}{x}^{(1)}{z}^{(2)}{z}^{(1)}+(x^{(2)}{)}^2(z^{(2)}{)}^2$ $=(x^{(1)}{)}^2(z^{(1)}{)}^2+2x^{(1)}{x}^{(2)}{z}^{(1)}{z}^{(2)}+(x^{(2)}{)}^2(z^{(2)}{)}^2$ 同样，这也正是 $K(\mathbf{x},\mathbf{z})$ 的展开形式。

结论：映射函数 $\Phi$ 的非唯一性 通过上述例子我们可以看出，对于同一个核函数 $K(\mathbf{x},\mathbf{z})$，可能存在多个不同形式的映射函数 $\Phi (\mathbf{x})$ 将数据映射到不同的特征空间。这再次强调了核技巧的强大之处：我们不需要关心 $\Phi$ 的具体形式，只要核函数本身是合法的（正定核），SVM 算法就可以正常工作。

7. 构建特征空间 (希尔伯特空间)

在线性支持向量机中，我们寻求的是在原始输入空间 $\mathcal{X}$ 中一个线性分离超平面。然而，当数据在原始空间中线性不可分时，我们提出将数据映射到一个更高维的特征空间 $\mathcal{H}$，在这个新空间中数据可能变得线性可分。这个特征空间 $\mathcal{H}$ 正是我们所说的希尔伯特空间。

7.1 什么是希尔伯特空间？

在之前的报告中，我们简要定义了希尔伯特空间。现在，让我们更细致地理解它：

一个希尔伯特空间 (Hilbert Space) 是一种具有特定性质的向量空间。它是一个完备的内积空间。 我们来拆解这个定义：

1. 向量空间 (Vector Space) / 线性空间 (Linear Space)：
   • 这是最基础的。一个集合如果定义了向量加法和标量乘法两种运算，且这些运算满足一系列公理（如结合律、分配律、零向量、负向量等），那么这个集合就是一个向量空间。
   • 这些运算必须是封闭的，即向量相加或向量与标量相乘的结果仍然在这个空间内。
2. 内积空间 (Inner Product Space)：
   • 在向量空间的基础上，如果定义了一个内积 (Inner Product) 运算，那么它就成为了一个内积空间。
   • 内积运算通常记作 $⟨f,g⟩$，它接受空间中的两个向量 $f$ 和 $g$，并返回一个标量。
   • 这个内积运算必须满足以下四个核心性质（我们将在稍后详细证明）：
     1. 对称性 (Symmetry)：$⟨f,g⟩=⟨g,f⟩$ （对于实数空间）。
     2. 线性性 (Linearity)：$⟨cf,g⟩=c⟨f,g⟩$ （标量乘法） 和 $⟨f+g,h⟩=⟨f,h⟩+⟨g,h⟩$ （加法）。
     3. 正定性 (Positive Definiteness)：$⟨f,f⟩\ge 0$，且 $⟨f,f⟩=0⟺f=0$。
3. 赋范线性空间 (Normed Linear Space)：
   • 一旦定义了内积，我们就可以通过内积来定义向量的范数 (Norm) 或“长度”：$\Vert f\Vert =\sqrt{⟨f,f⟩}$。
   • 一个定义了范数的向量空间就称为赋范线性空间。
4. 完备性 (Completeness)：
   • 这是希尔伯特空间区别于一般内积空间的关键。完备性意味着空间中所有柯西序列 (Cauchy sequence) 都收敛于该空间内的一个点。
   • 直观意义：完备性保证了我们可以进行极限操作，使得空间“没有漏洞”，在进行逼近或迭代时，结果不会“跳出”空间。在理论分析和算法收敛性证明中非常重要。

7.2 核函数如何构造这个空间？

在 SVM 中，我们实际上是通过核函数 $K(\mathbf{x},\mathbf{z})$ 来隐式地定义和构造这个特征空间 $\mathcal{H}$（一个再生核希尔伯特空间，Reproducing Kernel Hilbert Space, RKHS）。

1. 定义空间中的元素： 我们首先定义一个由核函数构成的函数集合 $S$。这个集合中的函数 $f(\cdot )$ 是有限个核函数 $K(\cdot ,{\mathbf{x}}_i)$ 的线性组合： $f(\cdot )={\sum }_{i=1}^m{\alpha }_{i}K(\cdot ,{\mathbf{x}}_i)$ 其中，${\alpha }_i\in \mathbb{R}$ 是实数系数，${\mathbf{x}}_i\in \mathcal{X}$ 是原始输入空间中的样本点（基点），$m$ 是一个有限正整数。这个集合 $S$ 是一个向量空间，因为有限个这样的函数相加或与标量相乘，结果仍然是这种形式的函数。
2. 定义内积运算： 对于 $S$ 中的任意两个函数 $f(\cdot )={\sum }_{i=1}^m{\alpha }_{i}K(\cdot ,{\mathbf{x}}_i)$ 和 $g(\cdot )={\sum }_{j=1}^l{\beta }_{j}K(\cdot ,{\mathbf{z}}_j)$，我们定义它们之间的内积为： $⟨f,g⟩={\sum }_{i=1}^m{\sum }_{j=1}^l{\alpha }_i{\beta }_{j}K({\mathbf{x}}_i,{\mathbf{z}}_j)$ 解释：这个定义是基于核函数的性质，它是一个巧妙的构造。它将两个函数之间的内积，转化为基点之间核函数值的线性组合。
3. 希尔伯特空间 (通过完备化)： 通过上述定义，我们得到了一个内积空间 $S$。如果我们将这个空间进行“完备化”（即填充所有柯西序列的极限点），我们就可以得到一个真正的希尔伯特空间 $\mathcal{H}$。这个 $\mathcal{H}$ 就是所谓的再生核希尔伯特空间 (RKHS)。

7.3 再生性 (Reproducing Property)

再生核希尔伯特空间有一个非常重要的性质叫做再生性 (Reproducing Property)。 对于任意 $\mathbf{x}\in \mathcal{X}$，定义函数 ${\Phi }_{\mathbf{x}}(\cdot )=K(\cdot ,\mathbf{x})$ (即核函数以 $\mathbf{x}$ 为第二个参数，第一个参数是变量)。 那么，对于任意 $f\in \mathcal{H}$，有： $⟨f,K(\cdot ,\mathbf{x})⟩=f(\mathbf{x})$ 我们来证明一下这个性质。设 $f(\cdot )={\sum }_{i=1}^m{\alpha }_{i}K(\cdot ,{\mathbf{x}}_i)$。 那么： $⟨f,K(\cdot ,\mathbf{x})⟩=⟨{\sum }_{i=1}^m{\alpha }_{i}K(\cdot ,{\mathbf{x}}_i),K(\cdot ,\mathbf{x})⟩$ 根据内积的线性性（我们稍后会证明）： $={\sum }_{i=1}^m{\alpha }_i⟨K(\cdot ,{\mathbf{x}}_i),K(\cdot ,\mathbf{x})⟩$ 根据内积的定义 $⟨K(\cdot ,\mathbf{u}),K(\cdot ,\mathbf{v})⟩=K(\mathbf{u},\mathbf{v})$（这是通过将 $K(\cdot ,\mathbf{u})$ 视为 $\sum {\delta }_{\mathbf{u}}K(\cdot ,\mathbf{u})$ 形式，其中 ${\delta }_{\mathbf{u}}$ 只有在索引为 $\mathbf{u}$ 时为 1，其他为 0 的系数，但更直接的证明需要从 $\Phi$ 映射的角度来理解 $K(\mathbf{u},\mathbf{v})=\Phi (\mathbf{u}{)}^T\Phi (\mathbf{v})$）： $={\sum }_{i=1}^m{\alpha }_{i}K({\mathbf{x}}_i,\mathbf{x})$ 由于核函数的对称性 $K({\mathbf{x}}_i,\mathbf{x})=K(\mathbf{x},{\mathbf{x}}_i)$： $={\sum }_{i=1}^m{\alpha }_{i}K(\mathbf{x},{\mathbf{x}}_i)$ 这正是函数 $f$ 在点 $\mathbf{x}$ 处的取值 $f(\mathbf{x})$。 所以，$⟨f,K(\cdot ,\mathbf{x})⟩=f(\mathbf{x})$。

再生性意味着，在 RKHS 中，对一个函数 $f$ 进行求值 $f(\mathbf{x})$，等价于计算它与核函数 $K(\cdot ,\mathbf{x})$ 的内积。这使得核函数在 RKHS 中扮演了“求值算子”的角色，也是其“再生”名称的由来。

8. 我们定义的运算是内积吗？ (内积的四个条件证明)

为了证明我们定义的运算 $⟨f,g⟩={\sum }_{i=1}^m{\sum }_{j=1}^l{\alpha }_i{\beta }_{j}K({\mathbf{x}}_i,{\mathbf{z}}_j)$ 确实是内积，我们需要逐一验证其满足四个条件。 设 $f(\cdot )={\sum }_{i=1}^m{\alpha }_{i}K(\cdot ,{\mathbf{x}}_i)$, $g(\cdot )={\sum }_{j=1}^l{\beta }_{j}K(\cdot ,{\mathbf{z}}_j)$, $h(\cdot )={\sum }_{k=1}^p{\gamma }_{k}K(\cdot ,{\mathbf{u}}_k)$。

8.1 条件 1：对称性

$⟨f,g⟩=⟨g,f⟩$ 证明： $⟨f,g⟩={\sum }_{i=1}^m{\sum }_{j=1}^l{\alpha }_i{\beta }_{j}K({\mathbf{x}}_i,{\mathbf{z}}_j)$ $⟨g,f⟩={\sum }_{j=1}^l{\sum }_{i=1}^m{\beta }_j{\alpha }_{i}K({\mathbf{z}}_j,{\mathbf{x}}_i)$ 由于实数的乘法交换律 (${\alpha }_i{\beta }_j={\beta }_j{\alpha }_i$) 和核函数的对称性 ($K({\mathbf{z}}_j,{\mathbf{x}}_i)=K({\mathbf{x}}_i,{\mathbf{z}}_j)$)，我们有： $⟨g,f⟩={\sum }_{j=1}^l{\sum }_{i=1}^m{\alpha }_i{\beta }_{j}K({\mathbf{x}}_i,{\mathbf{z}}_j)$ 由于求和顺序可以交换： $={\sum }_{i=1}^m{\sum }_{j=1}^l{\alpha }_i{\beta }_{j}K({\mathbf{x}}_i,{\mathbf{z}}_j)=⟨f,g⟩$ 结论：对称性成立。

8.2 条件 2：线性性 (两个子条件)

1. 标量乘法：$⟨cf,g⟩=c⟨f,g⟩$ (对于任意实数 $c$) 证明： 首先，函数 $cf(\cdot )=c{\sum }_{i=1}^m{\alpha }_{i}K(\cdot ,{\mathbf{x}}_i)={\sum }_{i=1}^m(c{\alpha }_i)K(\cdot ,{\mathbf{x}}_i)$。 那么，将 $c{\alpha }_i$ 视为新的系数，根据内积定义： $⟨cf,g⟩={\sum }_{i=1}^m{\sum }_{j=1}^l(c{\alpha }_i){\beta }_{j}K({\mathbf{x}}_i,{\mathbf{z}}_j)$ 由于实数乘法结合律： $=c{\sum }_{i=1}^m{\sum }_{j=1}^l{\alpha }_i{\beta }_{j}K({\mathbf{x}}_i,{\mathbf{z}}_j)$ $=c⟨f,g⟩$ 结论：标量乘法的线性性成立。

2. 加法：$⟨f+g,h⟩=⟨f,h⟩+⟨g,h⟩$ 证明： 首先，函数 $f(\cdot )+g(\cdot )={\sum }_{i=1}^m{\alpha }_{i}K(\cdot ,{\mathbf{x}}_i)+{\sum }_{j=1}^l{\beta }_{j}K(\cdot ,{\mathbf{z}}_j)$。 我们可以将 $f+g$ 视为一个包含 $m+l$ 个项的线性组合，其基点是 $\{{\mathbf{x}}_1,\dots ,{\mathbf{x}}_m,{\mathbf{z}}_1,\dots ,{\mathbf{z}}_l\}$。为了统一表示，假设我们有一个包含所有这些基点的大集合 $\{{\mathbf{u}}_1,\dots ,{\mathbf{u}}_{m+l}\}$，以及对应的系数 ${\gamma }_k^{\prime }$。 或者更直接地，根据内积的定义： $⟨f+g,h⟩=⟨{\sum }_{i=1}^m{\alpha }_{i}K(\cdot ,{\mathbf{x}}_i)+{\sum }_{j=1}^l{\beta }_{j}K(\cdot ,{\mathbf{z}}_j),{\sum }_{k=1}^p{\gamma }_{k}K(\cdot ,{\mathbf{u}}_k)⟩$ 这可以通过定义一个临时函数 $F=f+g$ 然后展开来证明，或者更严格地利用内积的分配律定义。 如果我们将内积定义为：$⟨{\sum }_a{c}_{a}K(\cdot ,{\mathbf{v}}_a),{\sum }_b{d}_{b}K(\cdot ,{\mathbf{w}}_b)⟩={\sum }_a{\sum }_b{c}_a{d}_{b}K({\mathbf{v}}_a,{\mathbf{w}}_b)$。 那么： $⟨f+g,h⟩=⟨{\sum }_{i=1}^m{\alpha }_{i}K(\cdot ,{\mathbf{x}}_i)+{\sum }_{j=1}^l{\beta }_{j}K(\cdot ,{\mathbf{z}}_j),h⟩$ 根据内积定义，这是将 $f+g$ 视为一个整体的线性组合，再与 $h$ 进行内积。 $={\sum }_{i=1}^m{\alpha }_i⟨K(\cdot ,{\mathbf{x}}_i),h⟩+{\sum }_{j=1}^l{\beta }_j⟨K(\cdot ,{\mathbf{z}}_j),h⟩$ （这里隐含使用了内积对第一个参数的线性性，如果直接从定义推导，需要更长的步骤） $⟨f,h⟩={\sum }_{i=1}^m{\sum }_{k=1}^p{\alpha }_i{\gamma }_{k}K({\mathbf{x}}_i,{\mathbf{u}}_k)$ $⟨g,h⟩={\sum }_{j=1}^l{\sum }_{k=1}^p{\beta }_j{\gamma }_{k}K({\mathbf{z}}_j,{\mathbf{u}}_k)$ $⟨f+g,h⟩={\sum }_{i=1}^m{\sum }_{k=1}^p{\alpha }_i{\gamma }_{k}K({\mathbf{x}}_i,{\mathbf{u}}_k)+{\sum }_{j=1}^l{\sum }_{k=1}^p{\beta }_j{\gamma }_{k}K({\mathbf{z}}_j,{\mathbf{u}}_k)$ 结论：加法的线性性成立。

8.3 条件 3：正定性

$⟨f,f⟩\ge 0\text{且}⟨f,f⟩=0⟺f=0$ 证明： $⟨f,f⟩=⟨{\sum }_{i=1}^m{\alpha }_{i}K(\cdot ,{\mathbf{x}}_i),{\sum }_{j=1}^m{\alpha }_{j}K(\cdot ,{\mathbf{x}}_j)⟩={\sum }_{i=1}^m{\sum }_{j=1}^m{\alpha }_i{\alpha }_{j}K({\mathbf{x}}_i,{\mathbf{x}}_j)$ 我们知道，一个函数 $K$ 如果是正定核，那么由任意有限点集 ${\mathbf{x}}_1,\dots ,{\mathbf{x}}_m$ 构成的 Gram 矩阵 $\mathbf{K}$ ($K_{ij}=K({\mathbf{x}}_i,{\mathbf{x}}_j)$) 必须是半正定矩阵。 设向量 $\mathbf{c}=({\alpha }_1,\dots ,{\alpha }_m{)}^T$。那么 ${\sum }_{i=1}^m{\sum }_{j=1}^m{\alpha }_i{\alpha }_{j}K({\mathbf{x}}_i,{\mathbf{x}}_j)$ 正好是二次型 ${\mathbf{c}}^T\mathbf{Kc}$。 由于 $\mathbf{K}$ 是半正定的，因此 ${\mathbf{c}}^T\mathbf{Kc}\ge 0$。所以 $⟨f,f⟩\ge 0$ 成立。

现在证明 $⟨f,f⟩=0⟺f=0$：

• ($\Leftarrow$) 如果 $f=0$： 如果 $f(\cdot )=0$（即对于所有 $\mathbf{x}\in \mathcal{X}$ 都有 $f(\mathbf{x})=0$），那么通过再生性： $⟨f,K(\cdot ,\mathbf{x})⟩=f(\mathbf{x})=0$。 $⟨f,f⟩=⟨f,{\sum }_{i=1}^m{\alpha }_{i}K(\cdot ,{\mathbf{x}}_i)⟩={\sum }_{i=1}^m{\alpha }_i⟨f,K(\cdot ,{\mathbf{x}}_i)⟩={\sum }_{i=1}^m{\alpha }_i\cdot 0=0$
• ($\Rightarrow$) 如果 $⟨f,f⟩=0$： 我们想证明这蕴含了 $f(\cdot )=0$。 由于 $⟨f,f⟩=0$，那么由内积性质，这等价于 $\Vert f\Vert =0$。 根据再生性：$|f(\mathbf{x})|=|⟨f,K(\cdot ,\mathbf{x})⟩|$。 通过柯西-施瓦茨不等式 (Cauchy-Schwarz inequality)：$|⟨f,g⟩|\le \Vert f\Vert \Vert g\Vert$。 $|f(\mathbf{x})|=|⟨f,K(\cdot ,\mathbf{x})⟩|\le \Vert f\Vert \Vert K(\cdot ,\mathbf{x})\Vert$ 如果 $\Vert f\Vert =0$，那么 $f(\mathbf{x})$ 必须为 0。所以 $f(\cdot )$ 是零函数。 结论：正定性成立。

总结：由于我们定义的运算满足内积的四个核心性质，因此它是一个内积。这证明了我们构造的函数集合 $S$ 是一个内积空间。

8. 正定核函数的充分必要条件 (Mercer 定理)

在之前的内容中，我们简要提到了 Mercer 定理。

定义：设 $K(\mathbf{x},\mathbf{z})$ 是定义在 $\mathcal{X}\times \mathcal{X}$ 上的一个对称函数。

• Mercer 定理 (充分必要条件)： $K(\mathbf{x},\mathbf{z})$ 是一个正定核函数（即存在一个希尔伯特空间 $\mathcal{H}$ 和一个映射 $\Phi :\mathcal{X}\to \mathcal{H}$ 使得 $K(\mathbf{x},\mathbf{z})=⟨\Phi (\mathbf{x}),\Phi (\mathbf{z}){⟩}_{\mathcal{H}}$），当且仅当，对于任意有限个样本点 ${\mathbf{x}}_1,\dots ,{\mathbf{x}}_m\in \mathcal{X}$，由 $K({\mathbf{x}}_i,{\mathbf{x}}_j)$ 构成的 Gram 矩阵 $\mathbf{K}=[K({\mathbf{x}}_i,{\mathbf{x}}_j){]}_{m\times m}$ 是半正定矩阵。

8.1 证明（必要性）：如果 $K$ 是核函数，则 Gram 矩阵是半正定的

假设：$K(\mathbf{x},\mathbf{z})$ 是一个核函数。这意味着存在一个映射 $\Phi :\mathcal{X}\to \mathcal{H}$（其中 $\mathcal{H}$ 是一个希尔伯特空间）使得 $K(\mathbf{x},\mathbf{z})=⟨\Phi (\mathbf{x}),\Phi (\mathbf{z}){⟩}_{\mathcal{H}}$。

目标：证明对于任意有限的样本点集 $\{{\mathbf{x}}_1,\dots ,{\mathbf{x}}_m\}$ 和任意实数 $c_1,\dots ,c_m$，以下二次型非负： ${\sum }_{i=1}^m{\sum }_{j=1}^m{c}_i{c}_{j}K({\mathbf{x}}_i,{\mathbf{x}}_j)\ge 0$

证明步骤：

1. 将 $K({\mathbf{x}}_i,{\mathbf{x}}_j)$ 替换为其在特征空间中的内积形式： ${\sum }_{i=1}^m{\sum }_{j=1}^m{c}_i{c}_{j}K({\mathbf{x}}_i,{\mathbf{x}}_j)={\sum }_{i=1}^m{\sum }_{j=1}^m{c}_i{c}_j⟨\Phi ({\mathbf{x}}_i),\Phi ({\mathbf{x}}_j){⟩}_{\mathcal{H}}$
2. 利用内积的线性性（对第二个参数的线性性，例如 $⟨u,v+w⟩=⟨u,v⟩+⟨u,w⟩$ 和 $⟨u,cv⟩=c⟨u,v⟩$）： $={\sum }_{i=1}^m{c}_i{⟨\Phi ({\mathbf{x}}_i),{\sum }_{j=1}^m{c}_j\Phi ({\mathbf{x}}_j)⟩}_{\mathcal{H}}$
3. 利用内积的对称性：$⟨u,v⟩=⟨v,u⟩$。 $={⟨{\sum }_{i=1}^m{c}_i\Phi ({\mathbf{x}}_i),{\sum }_{j=1}^m{c}_j\Phi ({\mathbf{x}}_j)⟩}_{\mathcal{H}}$ 解释：这里我们将求和项视为一个整体的向量 $\mathbf{V}={\sum }_{i=1}^m{c}_i\Phi ({\mathbf{x}}_i)$。那么整个表达式就是 $⟨\mathbf{V},\mathbf{V}{⟩}_{\mathcal{H}}$。
4. 根据内积的正定性定义，任何向量与自身的内积都必须是非负的（即范数的平方）： ${⟨{\sum }_{i=1}^m{c}_i\Phi ({\mathbf{x}}_i),{\sum }_{j=1}^m{c}_j\Phi ({\mathbf{x}}_j)⟩}_{\mathcal{H}}={\Vert {\sum }_{i=1}^m{c}_i\Phi ({\mathbf{x}}_i)\Vert }_{\mathcal{H}}^2\ge 0$ 结论：因此，如果 $K(\mathbf{x},\mathbf{z})$ 是一个核函数，那么由它构成的 Gram 矩阵必然是半正定的。这证明了 Mercer 定理的必要性。

8.2 证明（充分性）：如果 Gram 矩阵是半正定的，则 $K$ 是核函数

这部分证明涉及更高级的数学（如泛函分析和谱理论），但其核心思想是：如果 Gram 矩阵总是半正定的，那么我们可以构造出一个希尔伯特空间 $\mathcal{H}$ 和一个映射 $\Phi$ 使得 $K(\mathbf{x},\mathbf{z})=⟨\Phi (\mathbf{x}),\Phi (\mathbf{z}){⟩}_{\mathcal{H}}$。 这个构造通常就是我们前面讨论的再生核希尔伯特空间 (RKHS) 的构造，其中 $\Phi (\mathbf{x})$ 可以被定义为 $K(\cdot ,\mathbf{x})$ 本身在 RKHS 中的表示。

解释：这个“充分性”保证了只要我们能验证一个函数的 Gram 矩阵是半正定的，我们就可以放心地把它用作 SVM 的核函数，而无需显式地去找到那个高维映射 $\Phi$。这大大简化了核函数的选择和使用。

9. 常见的核函数类型 (Common Kernel Functions)

核函数是连接原始输入空间和高维特征空间的关键，它允许我们在不显式进行高维映射的情况下，完成分类或回归任务。不同的核函数对应着不同的隐式特征映射，因此它们能够捕捉数据中不同类型的非线性关系。

9.1 多项式核函数 (Polynomial Kernel)

多项式核函数通过计算输入特征的多项式组合来创建新的特征。它能够捕捉到数据中的多项式关系。

9.1.1 定义与参数

多项式核函数的标准形式为： $K(\mathbf{x},\mathbf{z})=(\gamma {\mathbf{x}}^T\mathbf{z}+r{)}^p$ 其中：

• $\mathbf{x},\mathbf{z}$ 是原始输入空间中的特征向量。
• ${\mathbf{x}}^T\mathbf{z}$ 是原始空间中的点积。
• $p$ (degree)：多项式的次数，一个正整数。它决定了特征空间中多项式项的最高次数。
• $\gamma$ (gamma)：核函数的系数，一个正实数。它控制了高阶项对内积的贡献。
• $r$ (coef0)：一个常数项（也称为截距或偏移量）。

9.1.2 隐式映射的直观理解与示例

为了理解多项式核如何进行隐式映射，我们以一个简单的例子进行推导。 设 $\mathbf{x}=(x_1,x_2{)}^T$ 和 $\mathbf{z}=(z_1,z_2{)}^T$。我们取 $p=2,\gamma =1,r=1$，即核函数为 $K(\mathbf{x},\mathbf{z})=({\mathbf{x}}^T\mathbf{z}+1{)}^2$。

步骤 1：展开核函数 $K(\mathbf{x},\mathbf{z})=({\mathbf{x}}^T\mathbf{z}+1{)}^2$ $=({\mathbf{x}}^T\mathbf{z}{)}^2+2({\mathbf{x}}^T\mathbf{z})+1$ 将点积 ${\mathbf{x}}^T\mathbf{z}=x_1{z}_1+x_2{z}_2$ 代入： $=(x_1{z}_1+x_2{z}_2{)}^2+2(x_1{z}_1+x_2{z}_2)+1$ 继续展开： $=(x_1{z}_1{)}^2+2(x_1{z}_1)(x_2{z}_2)+(x_2{z}_2{)}^2+2x_1{z}_1+2x_2{z}_2+1$ 重新排列项，将属于 $\mathbf{x}$ 和属于 $\mathbf{z}$ 的部分分开组合： $=(x_1^2)(z_1^2)+(\sqrt{2}{x}_1{x}_2)(\sqrt{2}{z}_1{z}_2)+(x_2^2)(z_2^2)+(\sqrt{2}{x}_1)(\sqrt{2}{z}_1)+(\sqrt{2}{x}_2)(\sqrt{2}{z}_2)+(1)(1)$

步骤 2：构造映射函数 $\Phi (\mathbf{x})$ 观察展开后的形式，它正是两个向量 $\Phi (\mathbf{x})$ 和 $\Phi (\mathbf{z})$ 的点积。 我们可以定义映射函数 $\Phi :{\mathbb{R}}^2\to {\mathbb{R}}^6$ 为： $\Phi (\mathbf{x})=(x_1^2,\sqrt{2}{x}_1{x}_2,x_2^2,\sqrt{2}{x}_1,\sqrt{2}{x}_2,1{)}^T$ 那么，$\Phi (\mathbf{x})\cdot \Phi (\mathbf{z})$ 恰好等于我们展开的 $K(\mathbf{x},\mathbf{z})$。

解释：

• 通过多项式核，原始的二维特征 $(x_1,x_2)$ 被映射到了一个六维的特征空间，包含了二次项（如 $x_1^2,x_1{x}_2,x_2^2$）、一次项（如 $x_1,x_2$）和常数项 (1)。
• 参数 $\gamma$ 实际上控制了线性项和高阶项的相对权重。
• 参数 $r$ 确保了映射后的特征空间包含常数项，并且当 $r>0$ 时，映射后的特征值通常不会太小，有助于数值稳定性。
• 参数 $p$ 直接决定了映射后的特征空间维度。随着 $p$ 的增大，特征空间的维度会急剧增加。

9.1.3 优点与缺点

• 优点：
  • 能够处理非线性数据，通过增加维度来寻找线性决策边界。
  • 在文本分类（词频特征）等领域有时表现良好。
• 缺点：
  • 参数选择敏感：$p$、$\gamma$ 和 $r$ 的选择对模型性能影响很大。特别是 $p$ 越大，维度越高，越容易过拟合。
  • 计算复杂度：对于高维输入，多项式核的计算可能会比较慢。
  • 数值稳定性：当输入特征值较大时，高次幂可能导致数值溢出。

9.2 高斯核函数 (Gaussian Kernel / Radial Basis Function, RBF Kernel)

高斯核函数是最常用的核函数之一，因为它能够将原始数据映射到无限维的特征空间，并且具有非常好的非线性建模能力。

9.2.1 定义与参数

高斯核函数的标准形式为： $K(\mathbf{x},\mathbf{z})=\exp (-\gamma \Vert \mathbf{x}-\mathbf{z}{\Vert }^2)$ 其中：

• $\mathbf{x},\mathbf{z}$ 是原始输入空间中的特征向量。
• $\Vert \mathbf{x}-\mathbf{z}{\Vert }^2$ 是两个向量之间的欧氏距离的平方（L2 范数的平方）。
• $\gamma$ (gamma)：核函数的带宽参数（或称为核宽、尺度参数），一个正实数。它决定了核函数的影响范围或“宽度”。

9.2.2 隐式映射的直观理解与特性

高斯核函数的隐式映射是无限维的，因此无法像多项式核那样简单地列出 $\Phi (\mathbf{x})$ 的所有维度。但我们可以从其相似度度量的角度来理解其直观意义。

• 相似度度量：高斯核函数衡量的是两个样本 $\mathbf{x}$ 和 $\mathbf{z}$ 之间的相似度。
  • 当 $\mathbf{x}$ 和 $\mathbf{z}$ 非常接近时，$\Vert \mathbf{x}-\mathbf{z}{\Vert }^2$ 接近 0，则 $K(\mathbf{x},\mathbf{z})=\exp (-\text{非常小的正数})$ 接近 $\exp (0)=1$。这意味着它们非常相似。
  • 当 $\mathbf{x}$ 和 $\mathbf{z}$ 距离很远时，$\Vert \mathbf{x}-\mathbf{z}{\Vert }^2$ 很大，则 $K(\mathbf{x},\mathbf{z})=\exp (-\text{非常大的正数})$ 接近 0。这意味着它们不相似。
• 局部性：高斯核具有很强的局部性 (Locality)。它的值随着距离的增加而指数级衰减。这意味着只有距离较近的样本才会对彼此的分类产生显著影响，而距离远的样本影响甚微。
• 参数 $\gamma$ 的作用：
  • $\gamma$ 很大：$\exp (-\gamma \Vert \mathbf{x}-\mathbf{z}{\Vert }^2)$ 衰减得非常快。这意味着只有距离极近的样本才会被认为是相似的，模型将变得非常“局部化”或“细致”。这可能导致过拟合，因为模型会为每个训练样本拟合一个非常小的区域，决策边界会变得非常复杂和不平滑。
  • $\gamma$ 很小：$\exp (-\gamma \Vert \mathbf{x}-\mathbf{z}{\Vert }^2)$ 衰减得非常慢。这意味着即使距离较远的样本也会被认为是相似的，模型将变得非常“全局化”或“粗糙”。这可能导致欠拟合，因为模型无法捕捉到数据的局部细节。

9.2.3 优点与缺点

• 优点：
  • 通用性强：高斯核是“通用核函数”（Universal Kernel），理论上它可以映射到任意维度的特征空间，并能够拟合任何复杂的决策边界（只要参数合适且有足够的数据）。
  • 参数较少：相比多项式核，它只有一个关键参数 $\gamma$ 需要调节，简化了参数选择。
  • 性能优异：在许多实际应用中，高斯核表现出色，是 SVM 中最常用的核函数。
• 缺点：
  • 对参数 $\gamma$ 敏感：尽管参数少，但 $\gamma$ 的选择对模型性能至关重要，通常需要通过交叉验证进行优化。
  • 无限维度挑战：虽然是隐式计算，但无限维度意味着所有数据点都会成为支持向量（在严格意义上），可能导致在预测时计算量增大（因为需要计算新样本与所有支持向量的核函数值）。
  • 解释性差：由于映射到无限维，很难直观地解释决策边界。

9.3 Sigmoid 核函数 (Sigmoid Kernel)

Sigmoid 核函数来源于神经网络中的 Sigmoid 激活函数，但它在 SVM 中不如多项式核和高斯核常用。

9.3.1 定义与参数

Sigmoid 核函数的标准形式为： $K(\mathbf{x},\mathbf{z})=\tanh (\gamma {\mathbf{x}}^T\mathbf{z}+r)$ 其中：

• $\tanh$ 是双曲正切函数，其输出范围是 $(-1,1)$。
• $\gamma ,r$ 是可调参数，与多项式核中的含义类似。

9.3.2 局限性

• 不总是正定核：Sigmoid 核函数只有在特定的参数 $\gamma$ 和 $r$ 取值下才能满足正定核的条件。这意味着它可能不总是一个有效的核函数，从而导致优化问题不收敛。
• 由于其不稳定的性质，在 SVM 实践中通常不推荐使用 Sigmoid 核函数。

---

10. 字符串核函数 (String Kernels)

到目前为止，我们讨论的核函数主要适用于欧几里得空间（数值向量） 中的数据。然而，在很多领域，我们的数据是非数值的，例如文本数据（单词序列）、DNA 序列、蛋白质序列等。这些数据无法直接表示为向量并使用点积。

字符串核函数正是为处理这类离散序列数据而设计的。它的核心思想是：衡量两个字符串的相似度，基于它们共享的子序列 (Subsequences)。

10.1 基本思想：共享子序列的计数

• 核心理念：将字符串隐式地映射到一个特征空间，这个特征空间的维度对应于所有可能的（或特定长度的）子序列。特征向量的每个维度代表一个特定子序列在字符串中出现的次数或某种加权统计。
• 核函数作用：通过计算这个高维特征空间中的内积，来量化两个字符串的相似度。

10.2 举例：子序列核 (Subsequence Kernel)

子序列核是最典型的字符串核函数之一。

10.2.1 定义概念

给定两个字符串 $S_1$ 和 $S_2$。一个长度为 $k$ 的子序列，是从一个字符串中按照原有顺序选择 $k$ 个字符得到的序列，这些字符在原字符串中可以不连续。

例如：字符串 “cat” 的长度为 2 的子序列有 “ca”, “ct”, “at”。

一个简单的子序列核函数可以定义为：所有长度为 $k$ 的公共子序列的数量。

更复杂的子序列核函数会引入加权机制： $K(S_1,S_2)=\frac{{\sum }_{u\in \mathcal{C}(S_1,S_2)}{\lambda }^{|u|}\cdot \text{count}(u,S_1)\cdot \text{count}(u,S_2)}{\sqrt{K(S_1,S_1)\cdot K(S_2,S_2)}}$ $\text{其中 }u\text{ 是 }{S}_1\text{ 和 }{S}_2\text{ 的公共子序列，}\mathcal{C}(S_1,S_2)\text{ 表示 }{S}_1\text{ 和 }{S}_2\text{ 的所有公共子序列集合}$ 或者更常见地，考虑子序列的 “不连续性惩罚” ： $K(S_1,S_2)={\sum }_{u\in {\Sigma }^k}{\sum }_{i:u=S_1[i_1\dots i_k]}{\sum }_{j:u=S_2[j_1\dots j_k]}{\lambda }^{{\sum }_{s=1}^k(i_{s+1}-i_s-1)+{\sum }_{s=1}^k(j_{s+1}-j_s-1)}$ 这里 $\lambda \in (0,1)$ 是一个衰减因子，$i_s$ 是子序列中第 $s$ 个字符在原字符串中的索引。惩罚项 ${\sum }_{s=1}^k(i_{s+1}-i_s-1)$ 衡量了子序列中字符之间的“跳跃”距离（gap）。

10.2.2 示例：计算子序列核

假设我们有一个简单的子序列核，它计算两个字符串共享的所有长度为 2 的子序列的计数，且不考虑跳跃惩罚。 考虑字符串 $S_1=\text{"cat"}$ 和 $S_2=\text{"cut"}$。

1. $S_1$ 的长度为 2 的子序列：
   • “ca” (索引 0, 1)
   • “ct” (索引 0, 2)
   • “at” (索引 1, 2)
2. $S_2$ 的长度为 2 的子序列：
   • “cu” (索引 0, 1)
   • “ct” (索引 0, 2)
   • “ut” (索引 1, 2)
3. 公共子序列： 唯一的公共子序列是 “ct”。
4. 核函数值： $K(S_1,S_2)=1$ (因为只有一个公共的长度为 2 的子序列)。 如果我们的核函数考虑长度为 1 的子序列，那么 “c”, “a”, “t” 和 “c”, “u”, “t” 共享 “c” 和 “t”，核函数值会更高。

10.2.3 字符串核的隐式映射 $\Phi (S)$

对于一个字符串 $S$，其隐式映射 $\Phi (S)$ 是一个非常高维的向量，其中每个维度对应一个特定的子序列 $u$。该维度的值通常是子序列 $u$ 在字符串 $S$ 中出现的加权计数。 $\Phi (S)=(\dots ,\text{count}(u_1,S),\text{count}(u_2,S),\dots {)}^T$ 其中 $\text{count}(u,S)$ 可以是 $u$ 在 $S$ 中出现的所有方式的 $\lambda$ 衰减和。 然后 $K(S_1,S_2)=\Phi (S_1{)}^T\Phi (S_2)$。

10.3 字符串核的挑战与应用

• 计算复杂性：所有可能的子序列的数量是指数级的，尤其对于长字符串。因此，直接计算或显式存储 $\Phi (S)$ 是不可能的。字符串核函数的设计需要巧妙的算法（例如使用动态规划）来高效地计算 $K(S_1,S_2)$。
• 参数选择：除了 SVM 本身的 $C$ 参数，字符串核函数通常还有长度参数 $k$ 和衰减参数 $\lambda$ 等，这些参数的选择也至关重要。
• 应用领域：
  • 文本分类：衡量文档或句子之间的相似性，例如垃圾邮件检测、情感分析。
  • 生物信息学：分析 DNA 序列、蛋白质序列之间的相似性，例如基因功能预测、蛋白质结构分类。
  • 自然语言处理：词性标注、命名实体识别等。