高斯混合模型

1. 概述

在许多实际场景中，我们观察到的数据可能并非来自一个单一的概率分布，而是由多个不同的、潜在的子群体生成的。例如：

• 身高数据：一个班级里，男生的身高可能服从一个正态分布，女生的身高服从另一个不同的正态分布。如果我们只观测到身高数据，而不知道性别，那么整个班级的身高分布看起来就像是两个正态分布的叠加。
• 客户行为：一个电商平台的客户购买行为可能由不同的消费群体（如“精打细算型”、“高消费型”、“冲动消费型”）生成，每个群体的购买金额、频率等特征可能服从不同的分布。

高斯混合模型（GMM） 正是为了应对这类问题而设计的。它假设观测数据是由 $K$ 个不同的高斯分量（Gaussian Components） 混合生成的，每个高斯分量代表一个潜在的子群体，并拥有自己的均值和方差（或协方差矩阵）。每个观测数据点都“属于”其中一个高斯分量，但我们并不知道它具体属于哪个分量，这正是GMM中的隐变量 。

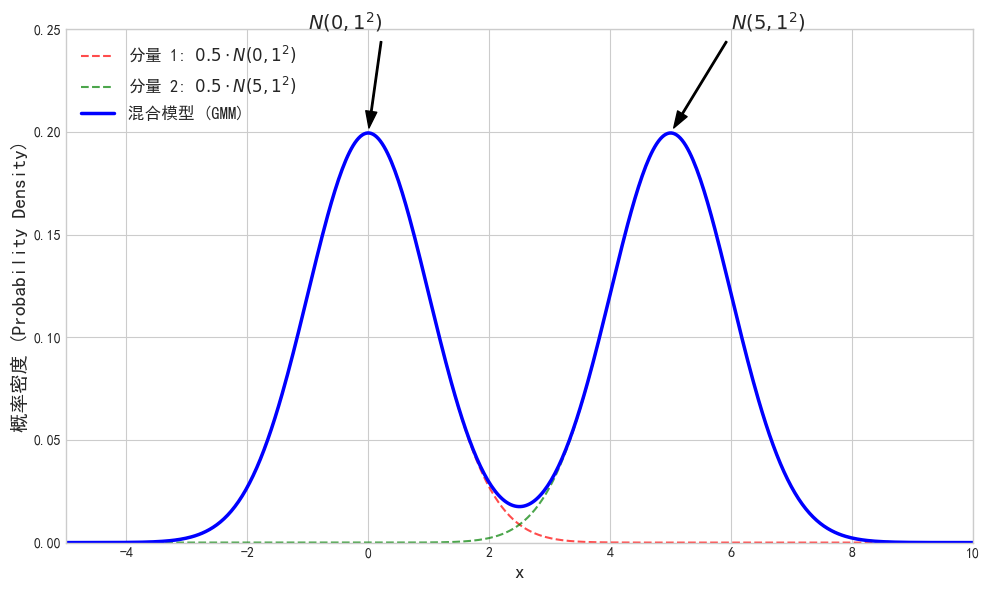
1.1 GMM的理解

想象我们在绘制数据点的直方图，发现它不是一个漂亮的钟形曲线，而是有多个“驼峰”（多峰分布），就像上面图片中展示的那样。这暗示着数据可能来自多个不同的“源”。

GMM的工作原理就是：

1. 假设存在多个“源”：这些“源”就是不同的高斯分布（每个分布对应一个钟形曲线）。
2. 每个源都有一个“权重”：表示数据来自这个源的可能性有多大（即混合系数）。
3. 最终分布是这些源的加权叠加：通过调整每个高斯的中心（均值）、宽度（方差）以及它们的权重，GMM试图最好地拟合观测数据的多峰形状。

2. 高斯混合模型的数学定义

2.1 模型构成

一个高斯混合模型由 $K$ 个高斯分量组成。每个分量 $k$ 都有：

• 混合系数（Mixture Coefficient）：${\alpha }_k$，表示数据点来自第 $k$ 个分量的概率。
  • 约束条件：${\sum }_{k=1}^K{\alpha }_k=1$ 且 ${\alpha }_k\ge 0$。
• 均值（Mean）：${\mu }_k$，表示第 $k$ 个高斯分量的中心。
• 方差（Variance）：${\sigma }_k^2$（在一维情况下）或协方差矩阵（Covariance Matrix） ${\Sigma }_k$（在多维情况下），表示第 $k$ 个高斯分量的“宽度”或“形状”。

GMM的参数集合为 $\theta =({\alpha }_1,\dots ,{\alpha }_K,{\mu }_1,\dots ,{\mu }_K,{\sigma }_1^2,\dots ,{\sigma }_K^2)$（对于多维数据，${\sigma }_k^2$ 替换为 ${\Sigma }_k$）。

2.2 观测数据与隐变量

• 观测数据 $Y$：我们实际收集到的数据点 $Y=\{y_1,y_2,\dots ,y_N\}$。每个 $y_j$ 是一个标量（一维）或向量（多维）。
• 隐变量 $Z$：对于每个观测数据点 $y_j$，我们并不知道它具体是由哪个高斯分量生成的。这个“来源”就是隐变量。
  • 我们引入一个隐变量 $z_j$，它是一个 $K$ 维的独热（one-hot）向量。如果 $y_j$ 是由第 $k$ 个高斯分量生成的，那么 $z_j$ 的第 $k$ 个分量为1，其余为0。
  • 例如，对于 $K=2$ 的情况，$z_j$ 可以是 $(1,0)$ 或 $(0,1)$。
  • 我们也可以用一个指示变量 ${\gamma }_{jk}$ 来表示 $z_j$ 的第 $k$ 个分量：
    • ${\gamma }_{jk}=1$ 如果 $y_j$ 来自第 $k$ 个分量。
    • ${\gamma }_{jk}=0$ 否则。
    • 显然，对于每个 $j$，${\sum }_{k=1}^K{\gamma }_{jk}=1$。

2.3 高斯混合模型的概率密度函数（PMF/PDF）

对于一个观测数据点 $y_j$，其概率密度函数（PDF）是所有 $K$ 个高斯分量的加权和：

$P(y_j|\theta )={\sum }_{k=1}^K{\alpha }_{k}P(y_j|\text{component }k,{\theta }_k)$

其中 $P(y_j|\text{component }k,{\theta }_k)$ 是第 $k$ 个高斯分量的概率密度函数 $\varphi (y_j|{\mu }_k,{\sigma }_k^2)$。

• 高斯分布（正态分布）的PDF： 对于一维随机变量 $y$，均值为 ${\mu }_k$，方差为 ${\sigma }_k^2$，其概率密度函数为：

  $\varphi (y|{\mu }_k,{\sigma }_k^2)=\frac{1}{\sqrt{2\pi }{\sigma }_k}\exp \left(-\frac{(y-{\mu }_k{)}^2}{2{\sigma }_k^2}\right)$

所以，GMM的概率密度函数为：

$P(y_j|\theta )={\sum }_{k=1}^K{\alpha }_k\frac{1}{\sqrt{2\pi }{\sigma }_k}\exp \left(-\frac{(y_j-{\mu }_k{)}^2}{2{\sigma }_k^2}\right)$

3. GMM的概率分布推导

为了应用EM算法，我们需要推导出完整数据的联合概率分布 $P(Y,Z|\theta )$。

3.1 单个完整数据点 $(y_j,z_j)$ 的联合概率

对于单个观测数据点 $y_j$ 和其对应的隐变量 $z_j$（指示 $y_j$ 来自哪个分量 $k$），其联合概率分布可以写为：

$P(y_j,z_j|\theta )=P(y_j|z_j,\theta )P(z_j|\theta )$

• $P(z_j|\theta )$：这是隐变量 $z_j$ 的先验概率，即选择第 $k$ 个分量的概率。如果 $z_j$ 的第 $k$ 个分量为1（表示 $y_j$ 来自分量 $k$），则 $P(z_j=k|\theta )={\alpha }_k$。
• $P(y_j|z_j,\theta )$：在已知 $y_j$ 来自第 $k$ 个分量的情况下，$y_j$ 的概率密度。这就是第 $k$ 个高斯分量的PDF：$\varphi (y_j|{\mu }_k,{\sigma }_k^2)$。

将这两个部分结合，使用指示变量 ${\gamma }_{jk}$ 来表示 $z_j$ 的第 $k$ 个分量为1：

$P(y_j,z_j|\theta )={\prod }_{k=1}^K[{\alpha }_k\varphi (y_j|{\mu }_k,{\sigma }_k^2){]}^{{\gamma }_{jk}}$

• 由于对于每个 $j$，只有一个 ${\gamma }_{jk}$ 是1，其余为0。所以这个乘积中只有一项是非1的，即对应于 $y_j$ 实际来源的那个分量 $k^{\prime }$ 的 ${\alpha }_{k^{\prime }}\varphi (y_j|{\mu }_{k^{\prime }},{\sigma }_{k^{\prime }}^2)$。 例如，如果 $y_j$ 来自第1个分量，那么 ${\gamma }_{j1}=1$, ${\gamma }_{j2}=\cdots ={\gamma }_{jK}=0$。则 $P(y_j,z_j|\theta )=[{\alpha }_1\varphi (y_j|{\mu }_1,{\sigma }_1^2){]}^1\cdot [{\alpha }_2\varphi (y_j|{\mu }_2,{\sigma }_2^2){]}^0\cdot \cdots ={\alpha }_1\varphi (y_j|{\mu }_1,{\sigma }_1^2)$。

3.2 完整数据集 $(Y,Z)$ 的联合概率分布

假设我们有 $N$ 个独立同分布的观测数据点，那么整个完整数据集 $Y=\{y_1,\dots ,y_N\}$ 和 $Z=\{z_1,\dots ,z_N\}$ 的联合概率分布就是所有单个数据点联合概率的乘积：

$$\begin{array}{rl}P(Y,Z|\theta )& =\prod _{j=1}^{N}P(y_j,z_j|\theta )\\ & =\prod _{j=1}^N\prod _{k=1}^K[{\alpha }_k\varphi (y_j|{\mu }_k,{\sigma }_k^2){]}^{{\gamma }_{jk}}\end{array}$$

这个公式表示了在给定参数 $\theta$ 的情况下，观测到所有 $Y$ 和所有 $Z$ 的概率。

3.3 完整数据对数似然函数 $L_c(\theta )$

为了方便求导和最大化，我们通常使用对数似然函数。对上述完整数据的联合概率取对数：

$$\begin{array}{rl}\log P(Y,Z|\theta )& =\log \prod _{j=1}^N\prod _{k=1}^K[{\alpha }_k\varphi (y_j|{\mu }_k,{\sigma }_k^2){]}^{{\gamma }_{jk}}\\ & =\sum _{j=1}^N\sum _{k=1}^K{\gamma }_{jk}\log [{\alpha }_k\varphi (y_j|{\mu }_k,{\sigma }_k^2)]\\ & =\sum _{j=1}^N\sum _{k=1}^K{\gamma }_{jk}[\log {\alpha }_k+\log \varphi (y_j|{\mu }_k,{\sigma }_k^2)]\\ & =\sum _{j=1}^N\sum _{k=1}^K{\gamma }_{jk}\log {\alpha }_k+\sum _{j=1}^N\sum _{k=1}^K{\gamma }_{jk}\log \varphi (y_j|{\mu }_k,{\sigma }_k^2)\end{array}$$

这个完整数据对数似然函数可以进一步简化：

• 交换求和顺序：

  ${\sum }_{j=1}^N{\sum }_{k=1}^K{\gamma }_{jk}\log {\alpha }_k={\sum }_{k=1}^K{\sum }_{j=1}^N{\gamma }_{jk}\log {\alpha }_k$

  对于每个 $k$，$\log {\alpha }_k$ 是常数，可以提到外面。而 ${\sum }_{j=1}^N{\gamma }_{jk}$ 正好是第 $k$ 个分量所包含的样本总数。我们记 $n_k={\sum }_{j=1}^N{\gamma }_{jk}$。 所以，第一项变为 ${\sum }_{k=1}^K{n}_k\log {\alpha }_k$。

最终，完整数据对数似然函数 $L_c(\theta )$ 为：

$L_c(\theta )={\sum }_{k=1}^K{n}_k\log {\alpha }_k+{\sum }_{j=1}^N{\sum }_{k=1}^K{\gamma }_{jk}\log \varphi (y_j|{\mu }_k,{\sigma }_k^2)$

4. GMM的EM算法实现

现在，我们有了完整数据对数似然的表达式，就可以应用EM算法来估计GMM的参数 $\theta =({\alpha }_k,{\mu }_k,{\sigma }_k^2)$ 了。

步骤 0：初始化参数 ${\theta }^{(0)}$ 随机初始化每个高斯分量的参数：

• 混合系数：${\alpha }_k^{(0)}$，确保 ${\sum }_{k=1}^K{\alpha }_k^{(0)}=1$。
• 均值：${\mu }_k^{(0)}$。
• 方差：${\sigma }_k^{2(0)}$。

步骤 1：E步

核心任务：计算隐变量 $z_j$ 的后验概率，即每个观测数据点 $y_j$ 属于第 $k$ 个高斯分量的概率。这个概率通常被称为责任，记作 ${\hat{\gamma }}_{jk}$（或 ${\gamma }_{jk}$ 或 $r_{jk}$）。

根据贝叶斯公式：

$$\begin{array}{rl}{\hat{\gamma }}_{jk}& =P(z_j=k|y_j,{\theta }^{(t)})\\ & =\frac{P(y_j|z_j=k,{\theta }^{(t)})P(z_j=k|{\theta }^{(t)})}{P(y_j|{\theta }^{(t)})}\\ & =\frac{\varphi (y_j|{\mu }_k^{(t)},{\sigma }_k^{2(t)}){\alpha }_k^{(t)}}{{\sum }_{l=1}^K\varphi (y_j|{\mu }_l^{(t)},{\sigma }_l^{2(t)}){\alpha }_l^{(t)}}\end{array}$$

• 分子：$\varphi (y_j|{\mu }_k^{(t)},{\sigma }_k^{2(t)}){\alpha }_k^{(t)}$ 表示在当前参数下，数据点 $y_j$ 由第 $k$ 个高斯分量生成的联合概率密度。
• 分母：${\sum }_{l=1}^K\varphi (y_j|{\mu }_l^{(t)},{\sigma }_l^{2(t)}){\alpha }_l^{(t)}$ 表示在当前参数下，数据点 $y_j$ 被观测到的总概率密度（对所有可能的分量求和）。

${\hat{\gamma }}_{jk}$ 是一个介于0和1之间的值，表示我们有多大的信心认为数据点 $y_j$ 是由第 $k$ 个高斯分量生成的。对于每个数据点 $y_j$，所有分量的责任之和为1：${\sum }_{k=1}^K{\hat{\gamma }}_{jk}=1$。 这些责任值 ${\hat{\gamma }}_{jk}$ 相当于三硬币模型中的 ${\mu }_j$（或 $1-{\mu }_j$），它们是我们在M步中用于加权估计参数的“期望的隐变量”。

构建Q函数： E步的最终目标是构建Q函数 $Q(\theta ,{\theta }^{(t)})=E_Z[\log P(Y,Z|\theta )|Y,{\theta }^{(t)}]$。 我们将完整数据对数似然函数 $L_c(\theta )$ 中的隐变量指示变量 ${\gamma }_{jk}$ 替换为其期望（即责任 ${\hat{\gamma }}_{jk}$）：

$Q(\theta ,{\theta }^{(t)})={\sum }_{k=1}^K{\hat{n}}_k\log {\alpha }_k+{\sum }_{j=1}^N{\sum }_{k=1}^K{\hat{\gamma }}_{jk}\log \varphi (y_j|{\mu }_k,{\sigma }_k^2)$

其中 ${\hat{n}}_k={\sum }_{j=1}^N{\hat{\gamma }}_{jk}$，表示第 $k$ 个分量在当前轮的有效样本数（所有数据点对第 $k$ 个分量的责任之和）。

步骤 2：M步（Maximization Step）

核心任务：最大化Q函数 $Q(\theta ,{\theta }^{(t)})$ 关于新的参数 $\theta =({\alpha }_k,{\mu }_k,{\sigma }_k^2)$。

2.1 估计混合系数 ${\alpha }_k^{(t+1)}$ 我们最大化Q函数中包含 ${\alpha }_k$ 的项，同时考虑约束 ${\sum }_{k=1}^K{\alpha }_k=1$。我们可以通过引入拉格朗日乘子（Lagrange Multiplier） 来解决。

我们需要最大化 $L_M(\alpha )={\sum }_{k=1}^K{\hat{n}}_k\log {\alpha }_k+\lambda ({\sum }_{k=1}^K{\alpha }_k-1)$。

对 ${\alpha }_k$ 求偏导并令其为0：

$\frac{\partial L_M}{\partial {\alpha }_k}=\frac{{\hat{n}}_k}{{\alpha }_k}+\lambda =0⟹{\alpha }_k=-\frac{{\hat{n}}_k}{\lambda }$

将所有 ${\alpha }_k$ 相加并利用 ${\sum }_{k=1}^K{\alpha }_k=1$：

${\sum }_{k=1}^K{\alpha }_k={\sum }_{k=1}^K-\frac{{\hat{n}}_k}{\lambda }=-\frac{1}{\lambda }{\sum }_{k=1}^K{\hat{n}}_k=1$

我们知道 ${\sum }_{k=1}^K{\hat{n}}_k={\sum }_{k=1}^K{\sum }_{j=1}^N{\hat{\gamma }}_{jk}={\sum }_{j=1}^N{\sum }_{k=1}^K{\hat{\gamma }}_{jk}={\sum }_{j=1}^{N}1=N$（所有数据点对所有分量的责任之和等于总样本数）。 所以，$-\frac{1}{\lambda }N=1⟹\lambda =-N$。 将 $\lambda =-N$ 代回 ${\alpha }_k$ 的表达式：

${\alpha }_k^{(t+1)}=\frac{{\hat{n}}_k}{N}=\frac{{\sum }_{j=1}^N{\hat{\gamma }}_{jk}}{N}$

新的混合系数 ${\alpha }_k$ 等于第 $k$ 个分量的有效样本数占总样本数的比例。这符合混合概率的直观理解。

2.2 估计均值 ${\mu }_k^{(t+1)}$ 我们最大化Q函数中包含 ${\mu }_k$ 的项：${\sum }_{j=1}^N{\sum }_{k=1}^K{\hat{\gamma }}_{jk}\log \varphi (y_j|{\mu }_k,{\sigma }_k^2)$。 只关注第 $k$ 个分量和 ${\mu }_k$：

$$\begin{array}{rl}\sum _{j=1}^N{\hat{\gamma }}_{jk}\log \left(\frac{1}{\sqrt{2\pi }{\sigma }_k}\exp \left(-\frac{(y_j-{\mu }_k{)}^2}{2{\sigma }_k^2}\right)\right)& =\sum _{j=1}^N{\hat{\gamma }}_{jk}\left(-\frac{1}{2}\log (2\pi )-\log {\sigma }_k-\frac{(y_j-{\mu }_k{)}^2}{2{\sigma }_k^2}\right)\end{array}$$

为了最大化，我们只需要最小化 ${\sum }_{j=1}^N{\hat{\gamma }}_{jk}(y_j-{\mu }_k{)}^2$。 对 ${\mu }_k$ 求偏导并令其为0：

$$\begin{array}{rl}\frac{\partial }{\partial {\mu }_k}\sum _{j=1}^N{\hat{\gamma }}_{jk}(y_j-{\mu }_k{)}^2& =\sum _{j=1}^N{\hat{\gamma }}_{jk}\cdot 2(y_j-{\mu }_k)\cdot (-1)=0\\ \sum _{j=1}^N{\hat{\gamma }}_{jk}(y_j-{\mu }_k)& =0\\ \sum _{j=1}^N{\hat{\gamma }}_{jk}{y}_j-\sum _{j=1}^N{\hat{\gamma }}_{jk}{\mu }_k& =0\\ \sum _{j=1}^N{\hat{\gamma }}_{jk}{y}_j& ={\mu }_k\sum _{j=1}^N{\hat{\gamma }}_{jk}\end{array}$$

所以，${\mu }_k$ 的更新公式为：

${\mu }_k^{(t+1)}=\frac{{\sum }_{j=1}^N{\hat{\gamma }}_{jk}{y}_j}{{\sum }_{j=1}^N{\hat{\gamma }}_{jk}}=\frac{{\sum }_{j=1}^N{\hat{\gamma }}_{jk}{y}_j}{{\hat{n}}_k}$

新的均值 ${\mu }_k$ 是所有数据点的加权平均，权重就是它们对第 $k$ 个分量的责任 ${\hat{\gamma }}_{jk}$。这符合加权平均值的定义。

2.3 估计方差 ${\sigma }_k^{2(t+1)}$ 同理，我们最大化Q函数中包含 ${\sigma }_k^2$ 的项。 对 ${\sigma }_k^2$ 求偏导并令其为0（或者对 ${\sigma }_k$ 求导，然后平方）：

$$\begin{array}{rl}\frac{\partial }{\partial {\sigma }_k}\sum _{j=1}^N{\hat{\gamma }}_{jk}\left(-\log {\sigma }_k-\frac{(y_j-{\mu }_k{)}^2}{2{\sigma }_k^2}\right)& =0\\ \sum _{j=1}^N{\hat{\gamma }}_{jk}\left(-\frac{1}{{\sigma }_k}+\frac{(y_j-{\mu }_k{)}^2}{{\sigma }_k^3}\right)& =0\\ \frac{1}{{\sigma }_k}\sum _{j=1}^N{\hat{\gamma }}_{jk}& =\frac{1}{{\sigma }_k^3}\sum _{j=1}^N{\hat{\gamma }}_{jk}(y_j-{\mu }_k{)}^2\\ {\sigma }_k^2\sum _{j=1}^N{\hat{\gamma }}_{jk}& =\sum _{j=1}^N{\hat{\gamma }}_{jk}(y_j-{\mu }_k{)}^2\end{array}$$

所以，${\sigma }_k^2$ 的更新公式为：

${\sigma }_k^{2(t+1)}=\frac{{\sum }_{j=1}^N{\hat{\gamma }}_{jk}(y_j-{\mu }_k^{(t+1)}{)}^2}{{\sum }_{j=1}^N{\hat{\gamma }}_{jk}}=\frac{{\sum }_{j=1}^N{\hat{\gamma }}_{jk}(y_j-{\mu }_k^{(t+1)}{)}^2}{{\hat{n}}_k}$

新的方差 ${\sigma }_k^2$ 是所有数据点到新均值 ${\mu }_k^{(t+1)}$ 的加权平方差的平均值，权重同样是它们对第 $k$ 个分量的责任 ${\hat{\gamma }}_{jk}$。

步骤 3：重复迭代 将新的参数估计 ${\theta }^{(t+1)}=({\alpha }_k^{(t+1)},{\mu }_k^{(t+1)},{\sigma }_k^{2(t+1)})$ 作为下一轮的初始值，然后重复E步和M步，直到参数收敛（例如，当参数变化量小于某个阈值时停止，或者对数似然函数的增长小于某个阈值）。