合页损失与线性支持向量机

线性支持向量机与合页损失 (Hinge Loss)

1. 损失函数在机器学习中的作用

在机器学习中，我们通常通过最小化一个损失函数 (Loss Function) 来训练模型。损失函数衡量模型预测值与真实值之间的“差距”或“误差”。最小化损失函数的目标，是找到一组模型参数，使得模型在训练数据上的表现尽可能好。

例如：

• 线性回归通常使用均方误差 (Mean Squared Error, MSE) 作为损失函数。
• 逻辑回归通常使用对数损失 (Log Loss / Cross-Entropy Loss)。

SVM 也不例外，它也可以被视为最小化一个特定的损失函数。

2. 回顾线性支持向量机的原始问题

从线性支持向量机而来，我们先回顾一下软间隔线性支持向量机的原始优化问题。给定训练数据集 $\{({\mathbf{x}}_1,y_1),\dots ,({\mathbf{x}}_N,y_N)\}$，其中 $y_i\in \{-1,+1\}$。问题形式为：

${\min }_{\mathbf{w},b,\mathbf{\xi }}\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C{\sum }_{i=1}^N{\xi }_i$ $\text{s.t.}{y}_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1-{\xi }_i\text{对于所有 }i=1,\dots ,N\text{ (约束 1)}$ ${\xi }_i\ge 0\text{对于所有 }i=1,\dots ,N\text{ (约束 2)}$

其中，${\xi }_i$ 是松弛变量，$C$ 是惩罚参数。

3. 定义合页损失 (Hinge Loss)

在讨论合页损失之前，我们先定义一个常用的操作符：正部函数 (Positive Part Function)。 $[z{]}_{+}=\max (0,z)=\{\begin{array}{ll}z& \text{如果 }z>0\\ 0& \text{如果 }z\le 0\end{array}$ 解释：这个函数简单地取输入值和 0 之间的较大者。如果输入是正数，就返回它本身；如果输入是负数或零，就返回 0。

现在，我们定义合页损失。对于一个样本 $({\mathbf{x}}_i,y_i)$，其损失定义为： $L_{\text{hinge}}(y_i,{\mathbf{w}}^T{\mathbf{x}}_i+b)=[1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b){]}_{+}$ 解释：

• 其中的 $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)$ 正是我们之前定义的函数间隔 ${\hat{\gamma }}_i$。
• 所以合页损失可以写成 $L_{\text{hinge}}({\hat{\gamma }}_i)=[1-{\hat{\gamma }}_i{]}_{+}$.
• 函数图像：
  • 当 ${\hat{\gamma }}_i\ge 1$ 时（即样本被正确分类且函数间隔大于或等于 1，位于间隔边界上或正确一侧），$1-{\hat{\gamma }}_i\le 0$。此时，合页损失为 $\max (0,\text{负数或零})=0$。这意味着当样本被“足够正确”地分类时，损失为零。
  • 当 ${\hat{\gamma }}_i<1$ 时（即样本位于间隔边界和决策超平面之间，或被错误分类），$1-{\hat{\gamma }}_i>0$。此时，合页损失为 $1-{\hat{\gamma }}_i$。损失随着函数间隔的减小而线性增加。

下图能够更清晰地展示合页损失的形状：

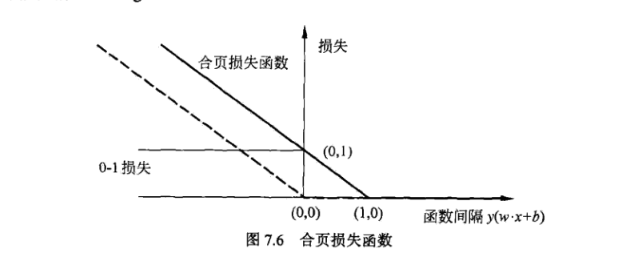
• 当函数间隔 $\ge 1$ 时，损失为 0。
• 当函数间隔 $<1$ 时，损失呈线性增加。

4. 松弛变量 ${\xi }_i$ 与合页损失的等价性

现在，我们来证明线性 SVM 原始问题中的松弛变量 ${\xi }_i$ 实际上等价于合页损失。

回顾松弛变量的定义和约束： $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1-{\xi }_i\text{ (约束 1)}$ ${\xi }_i\ge 0\text{ (约束 2)}$

我们可以将约束 1 重新整理一下： ${\xi }_i\ge 1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)$

现在，考虑原始优化问题的目标函数： ${\min }_{\mathbf{w},b,\mathbf{\xi }}\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C{\sum }_{i=1}^N{\xi }_i$ 我们要最小化 $\sum {\xi }_i$。在满足 ${\xi }_i\ge 1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)$ 和 ${\xi }_i\ge 0$ 这两个条件的前提下，为了使 $\sum {\xi }_i$ 尽可能小，每个 ${\xi }_i$ 的取值应该尽可能小。 因此，对于每个 ${\xi }_i$，它的最优取值将是满足这两个约束的最小值。 这个最小值恰好就是： ${\xi }_i=\max (0,1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b))$ 解释：

• 如果 $1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\le 0$（即 $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1$），那么为了最小化 ${\xi }_i$，我们取 ${\xi }_i=0$。这符合 $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1-0$。
• 如果 $1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)>0$（即 $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)<1$），那么为了最小化 ${\xi }_i$，我们取 ${\xi }_i=1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)$。这符合 $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1-(1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b))⟹y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)$，且 ${\xi }_i>0$。

所以，我们可以直接用 $\max (0,1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b))$ 来替换原始问题中的 ${\xi }_i$。

5. 将 SVM 原始问题表示为正则化经验风险最小化

将 ${\xi }_i=[1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b){]}_{+}$ 代入原始优化问题： ${\min }_{\mathbf{w},b}\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C{\sum }_{i=1}^N[1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b){]}_{+}$

这就是线性支持向量机从合页损失角度的理解！

• 正则化项 (Regularization Term)：$\frac{1}{2}\Vert \mathbf{w}{\Vert }^2$
  • 它旨在最小化模型复杂度，防止过拟合。这被称为 L2 正则化。最小化 $\Vert \mathbf{w}\Vert$ 实际上对应于最大化间隔。
• 经验风险项 (Empirical Risk Term)：$C{\sum }_{i=1}^N[1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b){]}_{+}$
  • 它衡量模型在训练数据上的分类损失，即模型拟合训练数据的程度。这里的损失函数就是合页损失。
  • 参数 $C$ 平衡了正则化项和经验风险项的重要性。

因此，==线性支持向量机可以被看作是一个在 L2 正则化下，最小化合页损失的优化问题。==

6. 合页损失与 0-1 损失的比较

在分类问题中，理想的损失函数是 0-1 损失 (Zero-One Loss)： $L_{0-1}(y,\text{sign}({\mathbf{w}}^T\mathbf{x}+b))=\{\begin{array}{ll}1& \text{如果 }y\ne \text{sign}({\mathbf{w}}^T\mathbf{x}+b)\\ 0& \text{如果 }y=\text{sign}({\mathbf{w}}^T\mathbf{x}+b)\end{array}$ 或者，用函数间隔表示： $L_{0-1}(\hat{\gamma })=\{\begin{array}{ll}1& \text{如果 }\hat{\gamma }\le 0\\ 0& \text{如果 }\hat{\gamma }>0\end{array}$ 解释：

• 当样本被错误分类时（函数间隔 $\hat{\gamma }\le 0$），损失为 1。
• 当样本被正确分类时（函数间隔 $\hat{\gamma }>0$），损失为 0。

为什么不直接优化 0-1 损失？ 因为 0-1 损失是一个非凸、不连续、不可微的函数。这意味着它有许多局部最小值，并且不能使用梯度下降等基于梯度的优化方法进行求解，是一个 NP-hard 问题。

合页损失作为 0-1 损失的“替代品”：

• 上界：合页损失是 0-1 损失的一个上界。
  • 当 $\hat{\gamma }\le 0$ 时，合页损失为 $1-\hat{\gamma }$，此时 $1-\hat{\gamma }\ge 1$。而 0-1 损失为 1。所以合页损失 $\ge$ 0-1 损失。
  • 当 $\hat{\gamma }>0$ 且 $\hat{\gamma }<1$ 时，合页损失为 $1-\hat{\gamma }$。而 0-1 损失为 0。所以合页损失 $\ge$ 0-1 损失。
  • 当 $\hat{\gamma }\ge 1$ 时，合页损失为 0。而 0-1 损失也为 0。所以合页损失 $=$ 0-1 损失。
• 凸性：合页损失是一个凸函数。这使得整个优化问题（$1/2\Vert \mathbf{w}{\Vert }^2$ 也是凸函数，凸函数之和仍是凸函数）成为一个凸优化问题，可以被高效地求解，并且能保证找到全局最优解。
• 间隔惩罚：合页损失对那些“分类正确但不够自信”的样本（即 $0<\hat{\gamma }<1$ 的样本）仍然施加惩罚，这符合 SVM 最大化间隔的思想。它促使模型不仅要正确分类，还要让样本尽可能远离决策边界，落在间隔之外。

总结

从合页损失的角度看线性 SVM，它提供了一个更通用的机器学习框架理解：

1. SVM 的原始优化问题（带松弛变量和约束）可以等价地转换为一个无约束的正则化经验风险最小化问题。
2. 在这个无约束问题中，L2 范数惩罚项 ($1/2\Vert \mathbf{w}{\Vert }^2$) 用于控制模型复杂度（最大化间隔），而合页损失 ($[1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b){]}_{+}$) 则作为衡量分类误差的损失函数。
3. 合页损失是一个凸函数，它作为理想但难以优化的 0-1 损失的凸替代品，使得 SVM 的优化问题变得可解且高效。同时，合页损失能够惩罚那些在间隔内部的样本，体现了 SVM 追求最大间隔的特性。