条件随机场（CRF）（二）：模型定义与参数化

1. 数学基础与符号约定

在深入CRF的公式之前，我们先明确一些基础概念和符号。这将帮助我们使用统一和严谨的语言进行讨论。

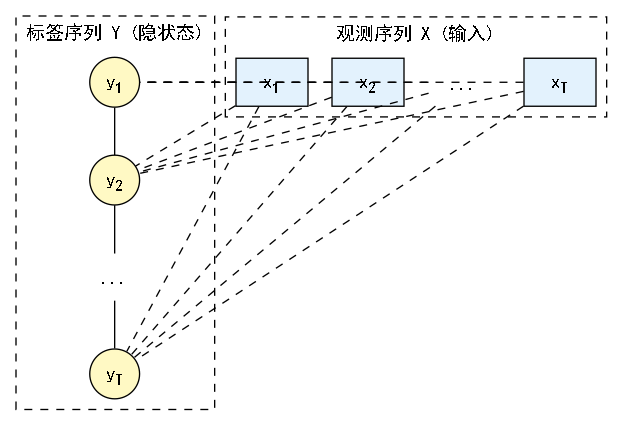
• 基本概念：无向图模型 (Undirected Graphical Model)

  • CRF是一种无向图模型，也称为马尔可夫随机场 (Markov Random Field, MRF)。
  • 它的核心思想是因子分解 (Factorization)：一个复杂的概率分布可以被分解为一系列定义在图中较小“局部”上的因子 (factor) 或势函数 (potential function) 的乘积。这些局部通常是图中的团 (clique)（即图中两两之间都有边连接的顶点子集）。
  • 对于线性链CRF，最关键的团就是相邻的两个标签节点，即边 $(y_{t-1},y_t)$。

• 符号约定

  • $X=(x_1,x_2,...,x_T)$：表示观测序列，即输入的句子中的 T 个词。
  • $Y=(y_1,y_2,...,y_T)$：表示标签序列，即我们希望预测的 T 个词性。
  • $t$：表示序列中的位置，从 1 到 T。
  • ${\Psi }_t(y_{t-1},y_t,X)$：表示在位置 $t$ 的势函数。它是一个非负实数，用于==衡量在给定整个观测序列 $X$ 的情况下，位置 $t-1$ 的标签为 $y_{t-1}$ 且位置 $t$ 的标签为 $y_t$ 这件事的“可能性”或“兼容性”有多高==。

2. 线性链CRF的严格定义

我们以最常见的线性链条件随机场 (Linear-chain CRF) 为例。它的图结构如下：

y1 ------ y2 ------ y3 ------ ... ------ yT

这里的 $y_t$ 是我们想预测的标签。CRF的核心在于，它假设条件概率 $p(Y|X)$ 的结构与这个图结构一致。根据无向图模型的因子分解理论，这个条件概率可以写成一系列定义在相邻标签对上的势函数的乘积，然后进行全局归一化。

线性链CRF的条件概率定义如下：

$$p(Y|X)=\frac{1}{Z(X)}\prod _{t=1}^T{\Psi }_t(y_{t-1},y_t,X)$$

让我们来逐一拆解这个公式的每个部分：

• ${\prod }_{t=1}^T{\Psi }_t(y_{t-1},y_t,X)$：非归一化概率

  • 这部分是模型的核心。它计算了特定标签序列 $Y$ 的“总分数”。
  • 这个分数是通过将序列中每一个相邻位置 $(t-1,t)$ 的“兼容性分数”（即势函数 ${\Psi }_t$ 的值）连乘得到的。
  • 关键点：注意每个势函数 ${\Psi }_t$ 的输入都包含了整个观测序列 $X$！这正是CRF能够利用全局特征的根本原因。

• $Z(X)$：归一化因子 (Normalization Factor)

  • $Z(X)$ 也被称为配分函数 (Partition Function)。
  • 它的作用是确保 $p(Y|X)$ 是一个合法的概率分布，即对于给定的 $X$，所有可能的标签序列 $Y^{\prime }$ 的概率之和为1。
  • 其定义为： $$Z(X)=\sum _{Y^{\prime }}\prod _{t=1}^T{\Psi }_t(y_{t-1}^{\prime },y_t^{\prime },X)$$
  • 深刻理解 $Z(X)$：这个公式的含义是，我们必须遍历所有可能的标签序列（比如一个长度为10的句子，每个词有3种词性，就有 $3^{10}$ 种序列），计算出每一种序列的“总分数”，然后把它们全部加起来，得到 $Z(X)$。
  • 这使得 $Z(X)$ 的计算通常非常昂贵，暴力计算是不可行的。这也正是后续我们要介绍的前向-后向算法要解决的核心问题。

3. 核心要素：特征函数 (Feature Functions)

现在，我们面临一个核心问题：势函数 ${\Psi }_t$ 到底是什么？它如何利用观测序列 $X$ 的信息？答案是通过特征函数 (Feature Functions) 和它们的权重 (Weights)。

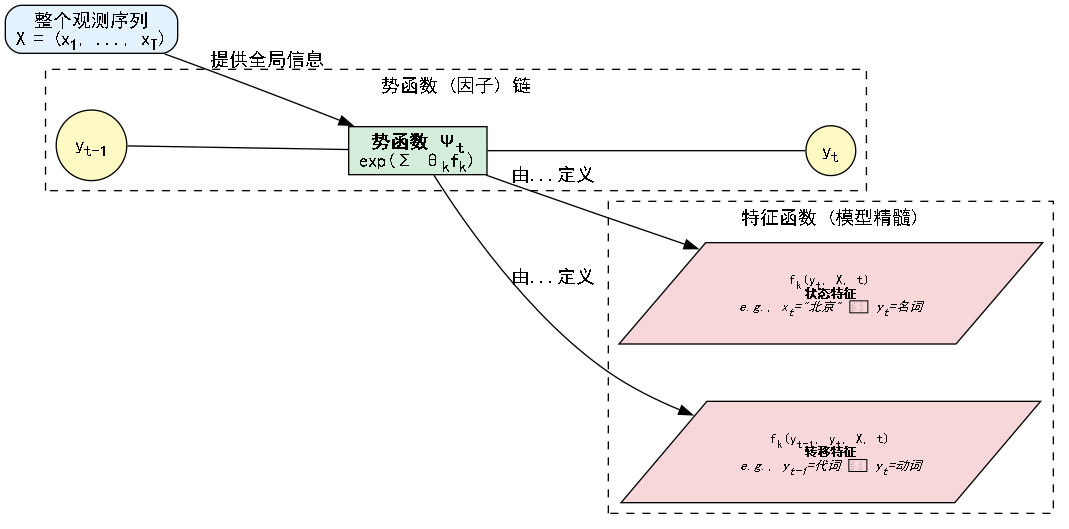
我们将势函数参数化为指数形式，这保证了其值非负，并且在数学上处理起来非常方便（属于指数族分布）：

$${\Psi }_t(y_{t-1},y_t,X)=\exp \left(\sum _{k=1}^K{\theta }_k{f}_k(y_{t-1},y_t,X,t)\right)$$

让我们再次拆解这个公式：

• $f_k(y_{t-1},y_t,X,t)$：第 $k$ 个特征函数

  • 这是CRF的精髓，也是模型效果好坏的关键。它由我们（模型设计者）来定义。
  • 它是一个实值函数（通常取值为0或1），用于从输入数据中提取某种我们认为有用的“模式”或“证据”。
  • 它的输入是：前一个标签 $y_{t-1}$，当前标签 $y_t$，整个观测序列 $X$，以及当前位置 $t$。
  • 它的输出代表了在当前位置 $t$，当标签为 $(y_{t-1},y_t)$ 时，某个特定模式是否被激活。

• ${\theta }_k$：第 $k$ 个特征函数的权重

  • 这是模型需要从训练数据中学习的参数。
  • 每个特征函数 $f_k$ 都对应一个权重 ${\theta }_k$。
  • 权重的直观含义是：
    • ${\theta }_k>0$ 且较大：表示特征 $f_k$ 是一个非常强的正面证据。当 $f_k$ 被激活时（值为1），它会大大增加其对应标签组合的概率。
    • ${\theta }_k<0$ 且较小：表示特征 $f_k$ 是一个非常强的负面证据。当 $f_k$ 被激活时，它会大大降低其对应标签组合的概率。
    • ${\theta }_k\approx 0$：表示特征 $f_k$ 几乎没有用，模型在决策时不会考虑它。

特征函数的设计示例

特征函数通常分为两类：

1. 状态特征 (State Feature)：只与当前标签 $y_t$ 有关。在形式上，它们是 $f_k(y_t,X,t)$，可以看作是 $f_k(y_{t-1},y_t,X,t)$ 中不依赖于 $y_{t-1}$ 的特例。

   • 例1 (词本身): $f_1(y_t,X,t)=1$, 如果 $y_t=\text{名词}$ 且 $x_t=\text{"北京"}$，否则为 0。 如果模型学到 ${\theta }_1$ 是一个很大的正数，意味着“北京”这个词极有可能是名词。

   • 例2 (词的形态): $f_2(y_t,X,t)=1$, 如果 $y_t=\text{动词}$ 且 $x_t$ 以 “ing” 结尾，否则为 0。 如果 ${\theta }_2$ 为正，模型就学会了 “ing” 词缀与动词有关。

   • 例3 (上下文信息): $f_3(y_t,X,t)=1$, 如果 $y_t=\text{名词}$ 且 $x_{t-1}=\text{"the"}$，否则为 0。 如果 ${\theta }_3$ 为正，模型就学会了冠词 “the” 后面很可能跟名词。

2. 转移特征 (Transition Feature)：与相邻标签 $y_{t-1}$ 和 $y_t$ 都有关。它捕捉了标签之间的依赖关系，类似于HMM中的转移概率。

   • 例4 (标签转移): $f_4(y_{t-1},y_t,X,t)=1$, 如果 $y_{t-1}=\text{代词}$ 且 $y_t=\text{动词}$，否则为 0。 如果 ${\theta }_4$ 为正，模型就学会了“代词-动词”是一个常见的标签组合。

总结一下：CRF的最终得分是所有被激活的特征函数的权重之和，再取指数。这个设计赋予了CRF巨大的灵活性和强大的建模能力。

4. CRF的简化与矩阵形式

为了方便后续的算法推导，我们通常会将CRF的定义式进行一些形式上的变换。

简化形式

将势函数的指数形式代入CRF的原始定义，我们可以利用 $\exp (a)\exp (b)=\exp (a+b)$ 的性质，将连乘的指数项合并为指数的连加项：

$$\begin{array}{rl}p(Y|X)& =\frac{1}{Z(X)}\prod _{t=1}^T\exp \left(\sum _{k=1}^K{\theta }_k{f}_k(y_{t-1},y_t,X,t)\right)\\ & =\frac{1}{Z(X)}\exp \left(\sum _{t=1}^T\sum _{k=1}^K{\theta }_k{f}_k(y_{t-1},y_t,X,t)\right)\end{array}$$

这个形式在推导学习算法（求导）时特别有用。

矩阵形式

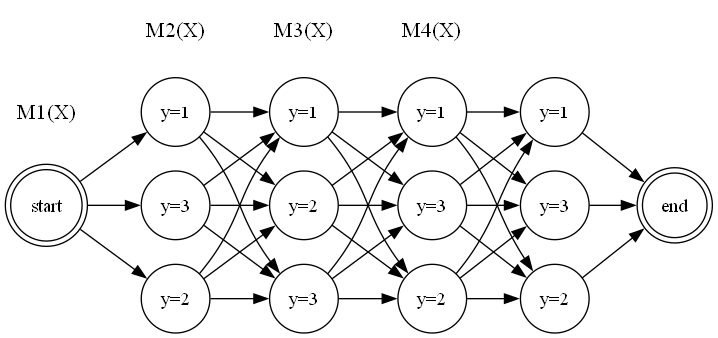
我们可以为序列中的每个位置 $t$ (从1到T) 定义一个 $M\times M$ 的转移矩阵 $M_t(X)$，其中 $M$ 是所有可能标签的数量（例如，词性有M种）。

矩阵 $M_t(X)$ 的第 $(i,j)$ 个元素定义为：

$$M_t(i,j)={\Psi }_t(y_{t-1}=i,y_t=j,X)=\exp \left(\sum _{k=1}^K{\theta }_k{f}_k(y_{t-1}=i,y_t=j,X,t)\right)$$

这个元素的含义是：在给定观测 $X$ 的条件下，从上一个位置的标签 $i$ 转移到当前位置的标签 $j$ 的非归一化分数。

有了这些矩阵，一个特定标签序列 $Y=(y_1,y_2,...,y_T)$ 的非归一化概率就可以表示为一系列矩阵元素的连乘：

$$\prod _{t=1}^T{M}_t(y_{t-1},y_t)$$

(注：这里需要定义一个虚拟的起始状态 $y_0$)

而归一化因子 $Z(X)$，即所有路径的非归一化概率之和，就可以通过矩阵连乘来计算：

$Z(X)=\text{row\_start}\cdot \left({\prod }_{t=1}^T{M}_t(X)\right)\cdot \text{col\_end}$

这个矩阵视角将看似复杂的全局求和问题，转化为了一个结构化的、可以通过动态规划高效求解的矩阵运算问题。这为我们之后要介绍的算法奠定了坚实的基础。

---

总结

在本文中，我们：

1. 严格定义了线性链CRF的条件概率公式，并理解了全局归一化因子 $Z(X)$ 的核心地位。
2. 深入剖析了CRF的灵魂——特征函数，理解了它是如何连接输入观测和输出标签的。
3. 掌握了CRF的参数化方式，即通过学习特征权重 ${\theta }_k$ 来构建模型。
4. 引入了CRF的矩阵形式，为后续高效的推断和学习算法做好了准备。

现在，我们已经完全理解了CRF模型本身。在条件随机场（CRF）（三）：三大核心问题之解码与概率计算 中，我们将学习如何在给定模型参数后，用它来解决实际问题。